Martin Görner
@martin-gorner.bsky.social
AI/ML engineer. Previously at Google: Product Manager for Keras and TensorFlow and developer advocate on TPUs. Passionate about democratizing Machine Learning.
Full report here: www.hottech.com/industry-cov...

Evaluating AI Inference Accelerators For Machine Vision Applications — Hot Tech
In a head-to-head battle of AI accelerators, the results are in — and Axelera AI didn’t just win, it ran laps around the competition.
www.hottech.com
July 16, 2025 at 3:51 PM
Full report here: www.hottech.com/industry-cov...
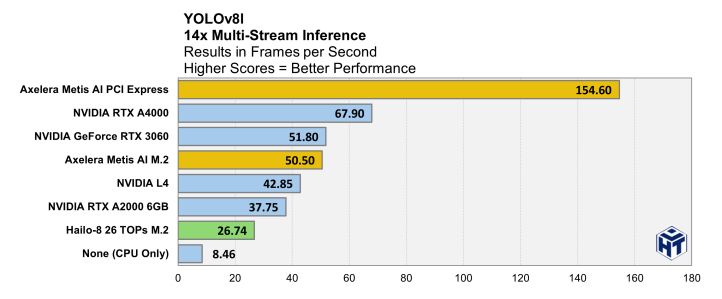
and check out the full report, which has data about more modern models like YOLO8L. For that model, compared to the best NVIDIA card tested, Axelera's Metis is:
- 230% faster
- 330% more power efficient
and also about 3x cheaper
- 230% faster
- 330% more power efficient
and also about 3x cheaper
July 16, 2025 at 3:42 PM
and check out the full report, which has data about more modern models like YOLO8L. For that model, compared to the best NVIDIA card tested, Axelera's Metis is:
- 230% faster
- 330% more power efficient
and also about 3x cheaper
- 230% faster
- 330% more power efficient
and also about 3x cheaper
4-chip Metis accelerator PCIe card coming soon:
store.axelera.ai/collections/...
store.axelera.ai/collections/...

PCIe AI accelerator card. Powered by 4 quad-core Metis AIPUs | Axelera AI Store
Axelera AI’s PCIe card, powered by 4 Metis AIPU, offers the highest performance inference acceleration on the market, combining ease of use, power efficiency, and scalability. Key Benefits: The highes...
store.axelera.ai
May 30, 2025 at 2:47 PM
4-chip Metis accelerator PCIe card coming soon:
store.axelera.ai/collections/...
store.axelera.ai/collections/...
PCIe and M.2 Metis boards available now:
- PCIe: axelera.ai/ai-accelerat...
- M.2: axelera.ai/ai-accelerat...
- PCIe: axelera.ai/ai-accelerat...
- M.2: axelera.ai/ai-accelerat...

Metis PCIe AI Inference Acceleration Card | Axelera AI
Looking for powerful & energy-efficient AI acceleration hardware that doesn't break budgets? Discover our PCIe AI inference accelerator card.
axelera.ai
May 30, 2025 at 2:47 PM
PCIe and M.2 Metis boards available now:
- PCIe: axelera.ai/ai-accelerat...
- M.2: axelera.ai/ai-accelerat...
- PCIe: axelera.ai/ai-accelerat...
- M.2: axelera.ai/ai-accelerat...
50+ models pre-configured in the model zoo are ready to run:
github.com/axelera-ai-h...
github.com/axelera-ai-h...
github.com
May 30, 2025 at 2:46 PM
50+ models pre-configured in the model zoo are ready to run:
github.com/axelera-ai-h...
github.com/axelera-ai-h...
I am impressed and humbled by what the Axelera team was able to bring to market, on only three years, with the Metis chip and Voyager SDK. And it's just a beginning. We have an exciting roadmap ahead! axelera.ai
Axelera AI - Extreme Performance, Excellent Efficiency. Accelerating Inference at the Edge.
Bring data insights to the edge, increasing the performance of your solutions with a cost-effective and efficient inference chip. Axelera’s AI processing unit is designed to seamlessly integrate into ...
axelera.ai
May 7, 2025 at 2:22 PM
I am impressed and humbled by what the Axelera team was able to bring to market, on only three years, with the Metis chip and Voyager SDK. And it's just a beginning. We have an exciting roadmap ahead! axelera.ai
The explosion of new AI models and capabilities, in advanced vision, speech recognition, language models, reasoning etc, needs a novel, energy-efficient approach to AI acceleration to deliver truly magical AI experiences, at the edge and in the datacenter.
May 7, 2025 at 2:22 PM
The explosion of new AI models and capabilities, in advanced vision, speech recognition, language models, reasoning etc, needs a novel, energy-efficient approach to AI acceleration to deliver truly magical AI experiences, at the edge and in the datacenter.
You'll see it in this form in Karpathy's original "Pong from pixel" post karpathy.github.io/2016/05/31/rl/ as well as my "RL without a PhD" video from a while ago youtu.be/t1A3NTttvBA.... They also explore a few basic reward assignment strategies.
Have fun, don't despair and RL!
Have fun, don't despair and RL!

TensorFlow and deep reinforcement learning, without a PhD (Google I/O '18)
On the forefront of deep learning research is a technique called reinforcement learning, which bridges the gap between academic deep learning problems and wa...
www.youtube.com
March 11, 2025 at 1:40 AM
You'll see it in this form in Karpathy's original "Pong from pixel" post karpathy.github.io/2016/05/31/rl/ as well as my "RL without a PhD" video from a while ago youtu.be/t1A3NTttvBA.... They also explore a few basic reward assignment strategies.
Have fun, don't despair and RL!
Have fun, don't despair and RL!
It is usually written in vector form, using the cross-entropy function. This time, I use 𝛑̅(sᵢₖ) for the *vector* of all move probabilities predicted from game state sᵢₖ, while 𝒙̅ᵢₖ is the one-hot encoded *vector* representing the move actually played in game i move k.
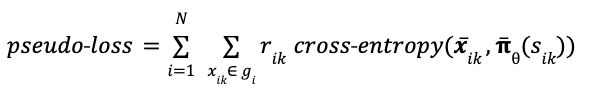
March 11, 2025 at 1:40 AM
It is usually written in vector form, using the cross-entropy function. This time, I use 𝛑̅(sᵢₖ) for the *vector* of all move probabilities predicted from game state sᵢₖ, while 𝒙̅ᵢₖ is the one-hot encoded *vector* representing the move actually played in game i move k.
One more thing: In modern autograd libraries like PyTorch or JAX, the RL gradient can be computed from the following “pseudo-loss”. Don’t try to find the meaning of this function, it does not have any. It’s just a function that has the gradient we want.
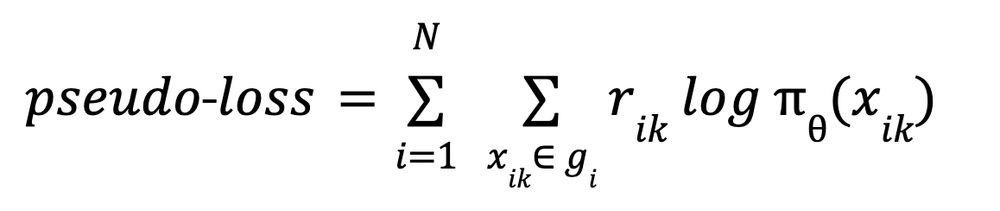
March 11, 2025 at 1:40 AM
One more thing: In modern autograd libraries like PyTorch or JAX, the RL gradient can be computed from the following “pseudo-loss”. Don’t try to find the meaning of this function, it does not have any. It’s just a function that has the gradient we want.
So in conclusion, math tells us that Reinforcement Learning is possible, even in multi-turn games where you cannot differentiate across multiple moves. But math tells us nothing about how to do it in practice. Which is why it is hard.

March 11, 2025 at 1:40 AM
So in conclusion, math tells us that Reinforcement Learning is possible, even in multi-turn games where you cannot differentiate across multiple moves. But math tells us nothing about how to do it in practice. Which is why it is hard.
What "rewards"? Well the "good" ones, that encourage the "correct" moves!
This is pretty much like a delicious recipe saying you should mix "great" ingredients in the "correct" proportions 😭. NOT HELPFUL AT ALL 🤬 !!!
This is pretty much like a delicious recipe saying you should mix "great" ingredients in the "correct" proportions 😭. NOT HELPFUL AT ALL 🤬 !!!
March 11, 2025 at 1:40 AM
What "rewards"? Well the "good" ones, that encourage the "correct" moves!
This is pretty much like a delicious recipe saying you should mix "great" ingredients in the "correct" proportions 😭. NOT HELPFUL AT ALL 🤬 !!!
This is pretty much like a delicious recipe saying you should mix "great" ingredients in the "correct" proportions 😭. NOT HELPFUL AT ALL 🤬 !!!
Now the bad news: what this equation really means is that the gradient we are looking for is the weighted sum of the gradients of our policy network over many individual games and moves, weighted by an unspecified set of “rewards”.
March 11, 2025 at 1:40 AM
Now the bad news: what this equation really means is that the gradient we are looking for is the weighted sum of the gradients of our policy network over many individual games and moves, weighted by an unspecified set of “rewards”.
We wanted to maximize the expected reward and managed to approximate the gradients form successive runs of the game, as played by our policy network. We can run backprop after all ... at least in theory 🙁.
March 11, 2025 at 1:40 AM
We wanted to maximize the expected reward and managed to approximate the gradients form successive runs of the game, as played by our policy network. We can run backprop after all ... at least in theory 🙁.
... string of zeros followed by the final reward - but we may have finer-grained rewarding strategies. The 1/N constant was folded into the rewards.
The good news: yay, This is computable 🎉🥳🎊! The expression only involves our policy network and our rewards.
The good news: yay, This is computable 🎉🥳🎊! The expression only involves our policy network and our rewards.
March 11, 2025 at 1:40 AM
... string of zeros followed by the final reward - but we may have finer-grained rewarding strategies. The 1/N constant was folded into the rewards.
The good news: yay, This is computable 🎉🥳🎊! The expression only involves our policy network and our rewards.
The good news: yay, This is computable 🎉🥳🎊! The expression only involves our policy network and our rewards.
For a more practical application, let's unroll the log-probabilities into individual moves using eq. (1) and rearrange a little. We use the fact that the log of a product is a sum of logs. I have also split the game reward into separate game steps rewards rᵢₖ - worst case a ...
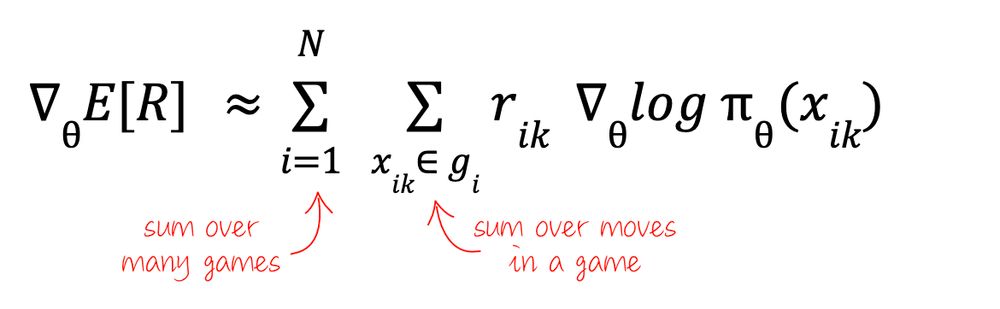
March 11, 2025 at 1:40 AM
For a more practical application, let's unroll the log-probabilities into individual moves using eq. (1) and rearrange a little. We use the fact that the log of a product is a sum of logs. I have also split the game reward into separate game steps rewards rᵢₖ - worst case a ...
But look, this is a sum of a probability × some value. That's an expectation! Which means that instead of computing it directly, we can approximate it from multiple games gᵢ :
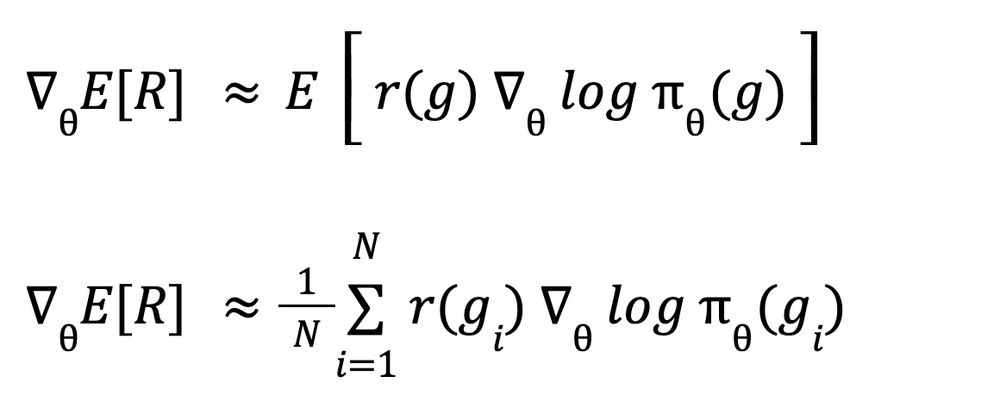
March 11, 2025 at 1:39 AM
But look, this is a sum of a probability × some value. That's an expectation! Which means that instead of computing it directly, we can approximate it from multiple games gᵢ :
And now we can start approximating like crazy - and abandon any pretense of doing exact math 😅.
First, we use our policy network 𝛑 to approximate the move probabilities.
First, we use our policy network 𝛑 to approximate the move probabilities.
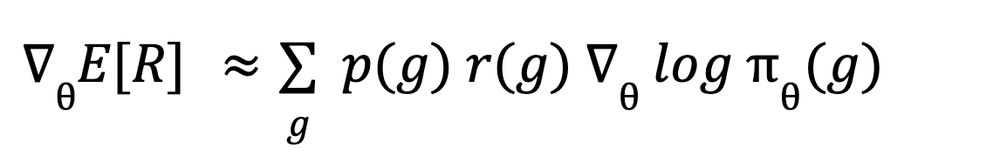
March 11, 2025 at 1:39 AM
And now we can start approximating like crazy - and abandon any pretense of doing exact math 😅.
First, we use our policy network 𝛑 to approximate the move probabilities.
First, we use our policy network 𝛑 to approximate the move probabilities.
Combining the last two equations we get:
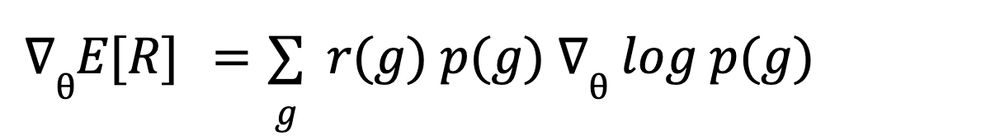
March 11, 2025 at 1:39 AM
Combining the last two equations we get:
We now use a mathematical cheap trick based on the fact that the derivative of log(x) is 1/x. With gradients, this cheap trick reads:

March 11, 2025 at 1:39 AM
We now use a mathematical cheap trick based on the fact that the derivative of log(x) is 1/x. With gradients, this cheap trick reads:
To maximize the expectation (3) we compute its gradient. The notation ∇ is the "gradient", or list of partial derivatives relatively to parameters θ. Differentiation is a linear operation so we can enter it into the sum Σ. Also, rewards do not depend on θ so:
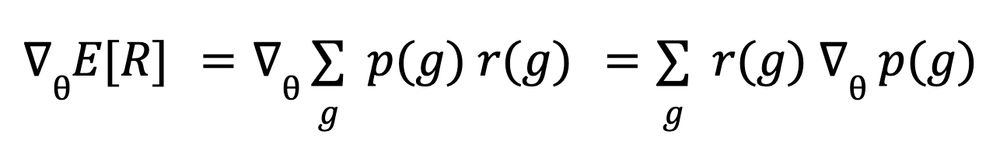
March 11, 2025 at 1:39 AM
To maximize the expectation (3) we compute its gradient. The notation ∇ is the "gradient", or list of partial derivatives relatively to parameters θ. Differentiation is a linear operation so we can enter it into the sum Σ. Also, rewards do not depend on θ so:

