Martin Görner
@martin-gorner.bsky.social
AI/ML engineer. Previously at Google: Product Manager for Keras and TensorFlow and developer advocate on TPUs. Passionate about democratizing Machine Learning.
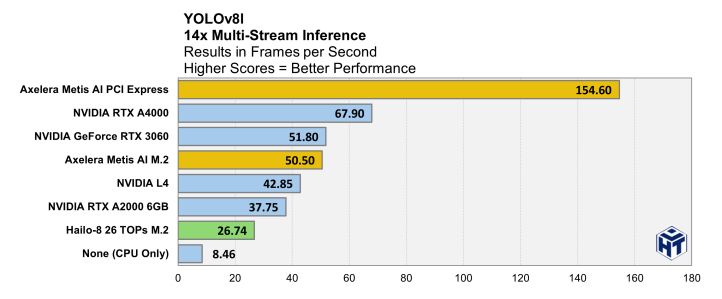
and check out the full report, which has data about more modern models like YOLO8L. For that model, compared to the best NVIDIA card tested, Axelera's Metis is:
- 230% faster
- 330% more power efficient
and also about 3x cheaper
- 230% faster
- 330% more power efficient
and also about 3x cheaper
July 16, 2025 at 3:42 PM
and check out the full report, which has data about more modern models like YOLO8L. For that model, compared to the best NVIDIA card tested, Axelera's Metis is:
- 230% faster
- 330% more power efficient
and also about 3x cheaper
- 230% faster
- 330% more power efficient
and also about 3x cheaper
I'm delighted to share that I joined the Axelera team this week to deliver the next generation AI compute platform. axelera.ai

May 7, 2025 at 2:21 PM
I'm delighted to share that I joined the Axelera team this week to deliver the next generation AI compute platform. axelera.ai
It is usually written in vector form, using the cross-entropy function. This time, I use 𝛑̅(sᵢₖ) for the *vector* of all move probabilities predicted from game state sᵢₖ, while 𝒙̅ᵢₖ is the one-hot encoded *vector* representing the move actually played in game i move k.
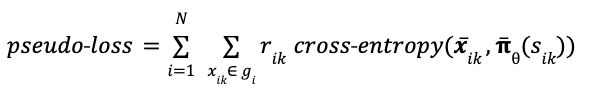
March 11, 2025 at 1:40 AM
It is usually written in vector form, using the cross-entropy function. This time, I use 𝛑̅(sᵢₖ) for the *vector* of all move probabilities predicted from game state sᵢₖ, while 𝒙̅ᵢₖ is the one-hot encoded *vector* representing the move actually played in game i move k.
One more thing: In modern autograd libraries like PyTorch or JAX, the RL gradient can be computed from the following “pseudo-loss”. Don’t try to find the meaning of this function, it does not have any. It’s just a function that has the gradient we want.
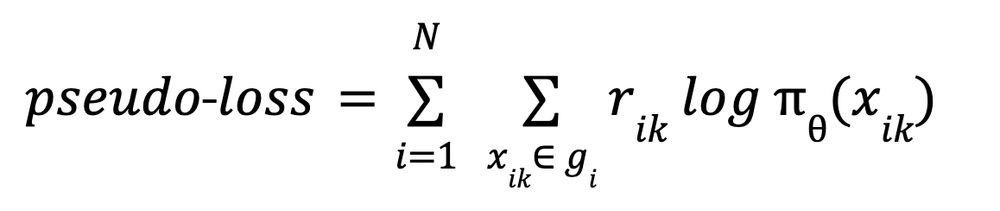
March 11, 2025 at 1:40 AM
One more thing: In modern autograd libraries like PyTorch or JAX, the RL gradient can be computed from the following “pseudo-loss”. Don’t try to find the meaning of this function, it does not have any. It’s just a function that has the gradient we want.
So in conclusion, math tells us that Reinforcement Learning is possible, even in multi-turn games where you cannot differentiate across multiple moves. But math tells us nothing about how to do it in practice. Which is why it is hard.

March 11, 2025 at 1:40 AM
So in conclusion, math tells us that Reinforcement Learning is possible, even in multi-turn games where you cannot differentiate across multiple moves. But math tells us nothing about how to do it in practice. Which is why it is hard.
For a more practical application, let's unroll the log-probabilities into individual moves using eq. (1) and rearrange a little. We use the fact that the log of a product is a sum of logs. I have also split the game reward into separate game steps rewards rᵢₖ - worst case a ...
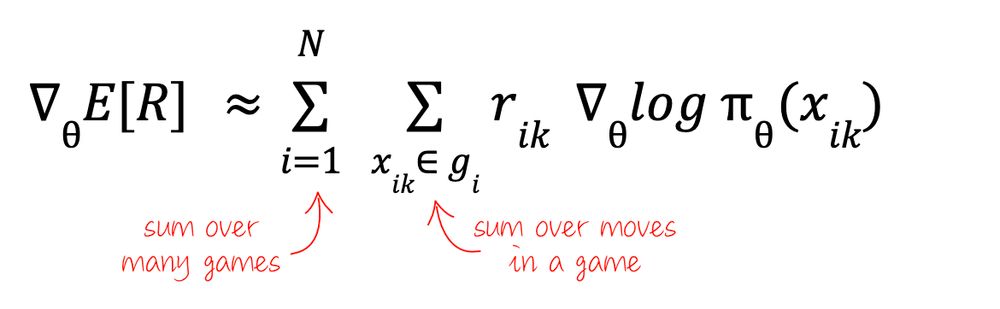
March 11, 2025 at 1:40 AM
For a more practical application, let's unroll the log-probabilities into individual moves using eq. (1) and rearrange a little. We use the fact that the log of a product is a sum of logs. I have also split the game reward into separate game steps rewards rᵢₖ - worst case a ...
But look, this is a sum of a probability × some value. That's an expectation! Which means that instead of computing it directly, we can approximate it from multiple games gᵢ :
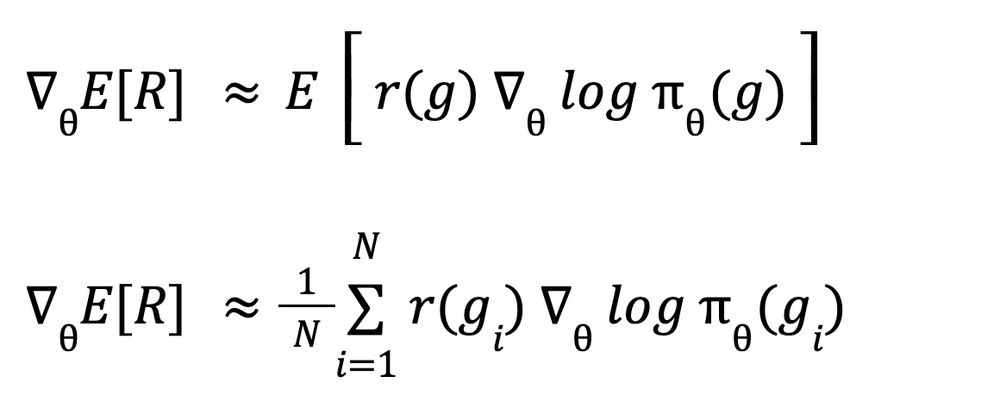
March 11, 2025 at 1:39 AM
But look, this is a sum of a probability × some value. That's an expectation! Which means that instead of computing it directly, we can approximate it from multiple games gᵢ :
And now we can start approximating like crazy - and abandon any pretense of doing exact math 😅.
First, we use our policy network 𝛑 to approximate the move probabilities.
First, we use our policy network 𝛑 to approximate the move probabilities.
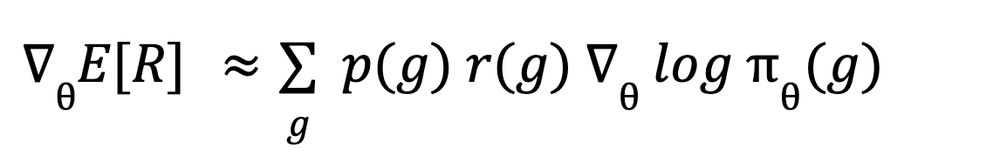
March 11, 2025 at 1:39 AM
And now we can start approximating like crazy - and abandon any pretense of doing exact math 😅.
First, we use our policy network 𝛑 to approximate the move probabilities.
First, we use our policy network 𝛑 to approximate the move probabilities.
Combining the last two equations we get:
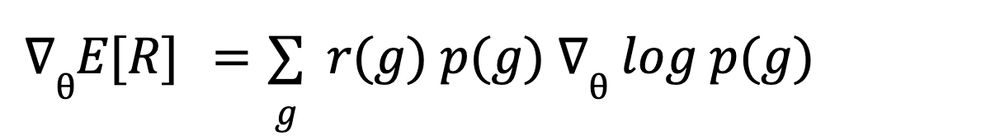
March 11, 2025 at 1:39 AM
Combining the last two equations we get:
We now use a mathematical cheap trick based on the fact that the derivative of log(x) is 1/x. With gradients, this cheap trick reads:

March 11, 2025 at 1:39 AM
We now use a mathematical cheap trick based on the fact that the derivative of log(x) is 1/x. With gradients, this cheap trick reads:
To maximize the expectation (3) we compute its gradient. The notation ∇ is the "gradient", or list of partial derivatives relatively to parameters θ. Differentiation is a linear operation so we can enter it into the sum Σ. Also, rewards do not depend on θ so:
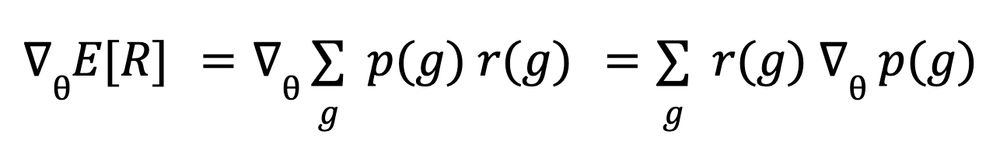
March 11, 2025 at 1:39 AM
To maximize the expectation (3) we compute its gradient. The notation ∇ is the "gradient", or list of partial derivatives relatively to parameters θ. Differentiation is a linear operation so we can enter it into the sum Σ. Also, rewards do not depend on θ so:
In probabilities, the “expectation” of a random variable X is the weighted sum of all possible outcomes xₖ, weighted by their probabilities p(xₖ). The really nice thing about expectations is that you can approximate them: just repeat the experiment and average the outcomes:
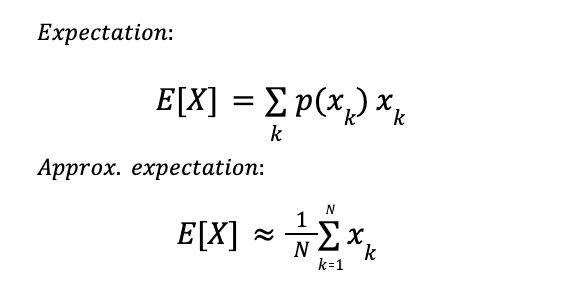
March 11, 2025 at 1:39 AM
In probabilities, the “expectation” of a random variable X is the weighted sum of all possible outcomes xₖ, weighted by their probabilities p(xₖ). The really nice thing about expectations is that you can approximate them: just repeat the experiment and average the outcomes:
Introducing the Reinforcement Learning ninja 🥷 hack: we can play many games and try and maximize the "expected reward". Yes, bear with me, this will end up being computable!
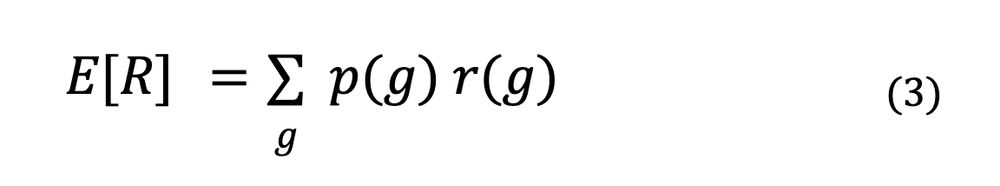
March 11, 2025 at 1:39 AM
Introducing the Reinforcement Learning ninja 🥷 hack: we can play many games and try and maximize the "expected reward". Yes, bear with me, this will end up being computable!
More formally, a "game" g is a sequence of game states s and moves x. Let's call r(g), the reward for the game. The probability of the game can be computed (I'll explain how shortly) from individual move probabilities which can in turn be predicted by a neural network.

March 11, 2025 at 1:39 AM
More formally, a "game" g is a sequence of game states s and moves x. Let's call r(g), the reward for the game. The probability of the game can be computed (I'll explain how shortly) from individual move probabilities which can in turn be predicted by a neural network.
You play until the outcome is clear, then assign a reward or penalty. With an LLM, this works for math or programming questions when the final answer can be verified. A slight refinement is when you can assign rewards to intermediate steps in the game (ORM vs. PRM, see pic⇩)


March 11, 2025 at 1:39 AM
You play until the outcome is clear, then assign a reward or penalty. With an LLM, this works for math or programming questions when the final answer can be verified. A slight refinement is when you can assign rewards to intermediate steps in the game (ORM vs. PRM, see pic⇩)
As often in machine learning, the math is both fun and, in the end, pretty useless 😝.
Let's set the stage: wether playing pong (single-player against a deterministic algorithm) or predicting the next token or sentence in a chain-of-thought LLM, the idea is the same:
Let's set the stage: wether playing pong (single-player against a deterministic algorithm) or predicting the next token or sentence in a chain-of-thought LLM, the idea is the same:
March 11, 2025 at 1:39 AM
As often in machine learning, the math is both fun and, in the end, pretty useless 😝.
Let's set the stage: wether playing pong (single-player against a deterministic algorithm) or predicting the next token or sentence in a chain-of-thought LLM, the idea is the same:
Let's set the stage: wether playing pong (single-player against a deterministic algorithm) or predicting the next token or sentence in a chain-of-thought LLM, the idea is the same:
Reinforcement Learning (RL) just landed a stellar breakthrough with reasoning language models. Yet, RL has a distinctly bad reputation. See “To RL or not to RL” (www.reddit.com/r/MachineLe...) on reddit.
I'd like to revisit the basic math of RL to see why. Let's enter the dungeon!
I'd like to revisit the basic math of RL to see why. Let's enter the dungeon!

March 11, 2025 at 1:39 AM
Reinforcement Learning (RL) just landed a stellar breakthrough with reasoning language models. Yet, RL has a distinctly bad reputation. See “To RL or not to RL” (www.reddit.com/r/MachineLe...) on reddit.
I'd like to revisit the basic math of RL to see why. Let's enter the dungeon!
I'd like to revisit the basic math of RL to see why. Let's enter the dungeon!
Quick sanity check: how diverse are the principal values of a pre-trained LLM?
Colab here, checking this on Gemma2 9B: colab.research.google.com/drive/1Igzf...
Bottom line: 99% of them are in the 0.1 - 1.1 range. I'm not sure partitioning them into "large" and "small" makes that much sense...
Colab here, checking this on Gemma2 9B: colab.research.google.com/drive/1Igzf...
Bottom line: 99% of them are in the 0.1 - 1.1 range. I'm not sure partitioning them into "large" and "small" makes that much sense...

February 20, 2025 at 12:39 PM
Quick sanity check: how diverse are the principal values of a pre-trained LLM?
Colab here, checking this on Gemma2 9B: colab.research.google.com/drive/1Igzf...
Bottom line: 99% of them are in the 0.1 - 1.1 range. I'm not sure partitioning them into "large" and "small" makes that much sense...
Colab here, checking this on Gemma2 9B: colab.research.google.com/drive/1Igzf...
Bottom line: 99% of them are in the 0.1 - 1.1 range. I'm not sure partitioning them into "large" and "small" makes that much sense...
- that truncating the bottom principal values from the SVD still offers a good approximation of the weights matrices
- that the fine-tuning data distribution if close to the pre-training one
Both questionable IMHO, so I won't detail the math.
Some results:
- that the fine-tuning data distribution if close to the pre-training one
Both questionable IMHO, so I won't detail the math.
Some results:

February 20, 2025 at 12:39 PM
- that truncating the bottom principal values from the SVD still offers a good approximation of the weights matrices
- that the fine-tuning data distribution if close to the pre-training one
Both questionable IMHO, so I won't detail the math.
Some results:
- that the fine-tuning data distribution if close to the pre-training one
Both questionable IMHO, so I won't detail the math.
Some results:
Finally, I'd like to mention LoRA-XS (arxiv.org/abs/2405.17604). Very similar to PiSSA but slightly different mechanism. Also good results with significantly fewer params than LoRA. The paper offers a mathematical explanation of why this setup is "ideal' under two conditions:

February 20, 2025 at 12:39 PM
Finally, I'd like to mention LoRA-XS (arxiv.org/abs/2405.17604). Very similar to PiSSA but slightly different mechanism. Also good results with significantly fewer params than LoRA. The paper offers a mathematical explanation of why this setup is "ideal' under two conditions:
The PiSSA paper also has an interesting finding: full fine-tuning is prone to over-fitting. You might get better results in the absolute with a low-rank fine-tuning technique.

February 20, 2025 at 12:39 PM
The PiSSA paper also has an interesting finding: full fine-tuning is prone to over-fitting. You might get better results in the absolute with a low-rank fine-tuning technique.
Surprisingly, MiLoRA seems to have the upper hand, at least when tuning on math datasets which are probably fairly aligned with the original pre-training. Arguably, PiSSA should be better for bending the behavior of the LLM further from its pre-training.

February 20, 2025 at 12:39 PM
Surprisingly, MiLoRA seems to have the upper hand, at least when tuning on math datasets which are probably fairly aligned with the original pre-training. Arguably, PiSSA should be better for bending the behavior of the LLM further from its pre-training.
From the paper: "PiSSA is designed to approximate full finetuning by adapting the principal singular components, which are believed to capture the essence of the weight matrices. In contrast, MiLoRA aims to adapt to new tasks while maximally retaining the base model’s knowledge."

February 20, 2025 at 12:39 PM
From the paper: "PiSSA is designed to approximate full finetuning by adapting the principal singular components, which are believed to capture the essence of the weight matrices. In contrast, MiLoRA aims to adapt to new tasks while maximally retaining the base model’s knowledge."
Two papers have explored what happens if you tune only the large singular values or only the small ones: PiSSA (Principal Singular val. Adaptation arxiv.org/abs/2404.02948) and MiLoRA (Minor singular component LoRA arxiv.org/abs/2406.09044).

February 20, 2025 at 12:39 PM
Two papers have explored what happens if you tune only the large singular values or only the small ones: PiSSA (Principal Singular val. Adaptation arxiv.org/abs/2404.02948) and MiLoRA (Minor singular component LoRA arxiv.org/abs/2406.09044).
... the USVt form on one hand, the Σs(i)u(i)vt(i) on the other, simplify using the fact that S is diagonal and notice that it's the same thing).
In this representation, it's easy to see that you can split the sum in two. And this is what the split looks like on matrices:
In this representation, it's easy to see that you can split the sum in two. And this is what the split looks like on matrices:

February 20, 2025 at 12:39 PM
... the USVt form on one hand, the Σs(i)u(i)vt(i) on the other, simplify using the fact that S is diagonal and notice that it's the same thing).
In this representation, it's easy to see that you can split the sum in two. And this is what the split looks like on matrices:
In this representation, it's easy to see that you can split the sum in two. And this is what the split looks like on matrices:

