





One plasticity rule improved learning, but its weight updates weren't aligned with backprop's. It was doing something different. That rule is Oja's plasticity rule.

One plasticity rule improved learning, but its weight updates weren't aligned with backprop's. It was doing something different. That rule is Oja's plasticity rule.

1) large negative eigenvalues are not necessary for LRS, and
2) high-dim input and stable dynamics are not sufficient for high-dim responses.
Motivated by this conversation, I added eigenvalues to the plot and edited the text a bit, thx!
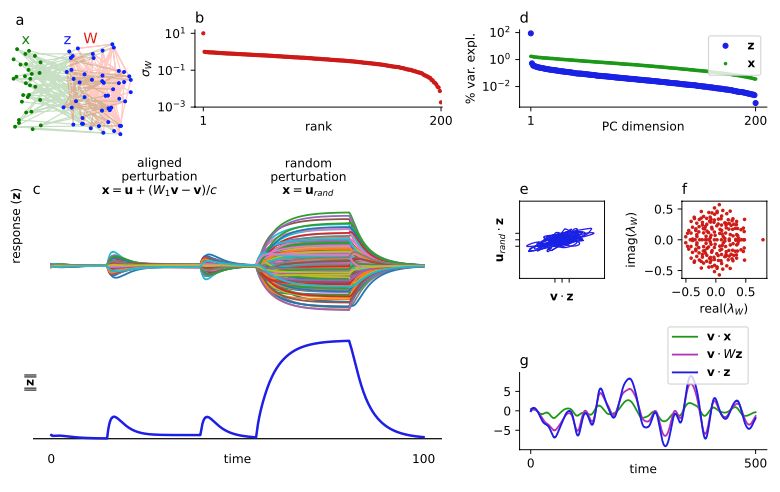
1) large negative eigenvalues are not necessary for LRS, and
2) high-dim input and stable dynamics are not sufficient for high-dim responses.
Motivated by this conversation, I added eigenvalues to the plot and edited the text a bit, thx!
Attached is an example (Fig 2d,e in paper) with pos and neg overlaps (P is the overlap matrix).

Attached is an example (Fig 2d,e in paper) with pos and neg overlaps (P is the overlap matrix).
For example, LRS is very general, occurs in the attached example where the dominant left- and right singular vectors are near-orthogonal. E-vals are negative, but O(1) in magnitude, not separated from bulk.

For example, LRS is very general, occurs in the attached example where the dominant left- and right singular vectors are near-orthogonal. E-vals are negative, but O(1) in magnitude, not separated from bulk.
LRS is defined as the presence of a small number of suppressed directions (the last blue dot in the var expl figure we are replying to).
High-dim responses is the absence of a small number of amplified directions.
I attached our assumptions and conditions for each.

LRS is defined as the presence of a small number of suppressed directions (the last blue dot in the var expl figure we are replying to).
High-dim responses is the absence of a small number of amplified directions.
I attached our assumptions and conditions for each.
If we account for this, the network produces high-dim dynamics.
And the network is more sensitive to random perturbations than to perturbations aligned to the low dim structure.

If we account for this, the network produces high-dim dynamics.
And the network is more sensitive to random perturbations than to perturbations aligned to the low dim structure.
Due to low-rank suppression these networks amplify spatially disordered inputs relative to spatially smooth ones.

Due to low-rank suppression these networks amplify spatially disordered inputs relative to spatially smooth ones.
Due to low-rank suppression, these networks amplify random input relative to inputs that are homogeneous within each module.
This effect is related to E-I balance in neural circuits.

Due to low-rank suppression, these networks amplify random input relative to inputs that are homogeneous within each module.
This effect is related to E-I balance in neural circuits.
The steady state is determined by the input through multiplication by the inverse of the network's connectivity matrix.

The steady state is determined by the input through multiplication by the inverse of the network's connectivity matrix.
One is aligned to the low dimensional structure of the network.
The other is random.
Perhaps surprisingly, the network's response to the aligned stimulus is suppressed relative to the random one.

One is aligned to the low dimensional structure of the network.
The other is random.
Perhaps surprisingly, the network's response to the aligned stimulus is suppressed relative to the random one.
Notice the last PC of the dynamics (last blue dot):
There is an abrupt jump downward in var explained.
This is caused by an effect we call "low-rank suppression"

Notice the last PC of the dynamics (last blue dot):
There is an abrupt jump downward in var explained.
This is caused by an effect we call "low-rank suppression"
The variance explained by the principal components of the network dynamics (blue) decayed slowly, reflecting those of of the stimulus (green), but not the network structure (red above).

The variance explained by the principal components of the network dynamics (blue) decayed slowly, reflecting those of of the stimulus (green), but not the network structure (red above).
We perturbed the network with a high-dimensional input (iid smooth Gaussian noise).

We perturbed the network with a high-dimensional input (iid smooth Gaussian noise).
High-dimensional stimuli produce high-dimensional dynamics.

High-dimensional stimuli produce high-dimensional dynamics.

New preprint with a former undergrad, Yue Wan.
I'm not totally sure how to talk about these results. They're counterintuitive on the surface, seem somewhat obvious in hindsight, but then there's more to them when you dig deeper.

New preprint with a former undergrad, Yue Wan.
I'm not totally sure how to talk about these results. They're counterintuitive on the surface, seem somewhat obvious in hindsight, but then there's more to them when you dig deeper.

The book assumes no background in biology, only a basic background in math (e.g., calculus and matrices).
All other mathematical background is covered in an appendix.
(3/n)

The book assumes no background in biology, only a basic background in math (e.g., calculus and matrices).
All other mathematical background is covered in an appendix.
(3/n)

