
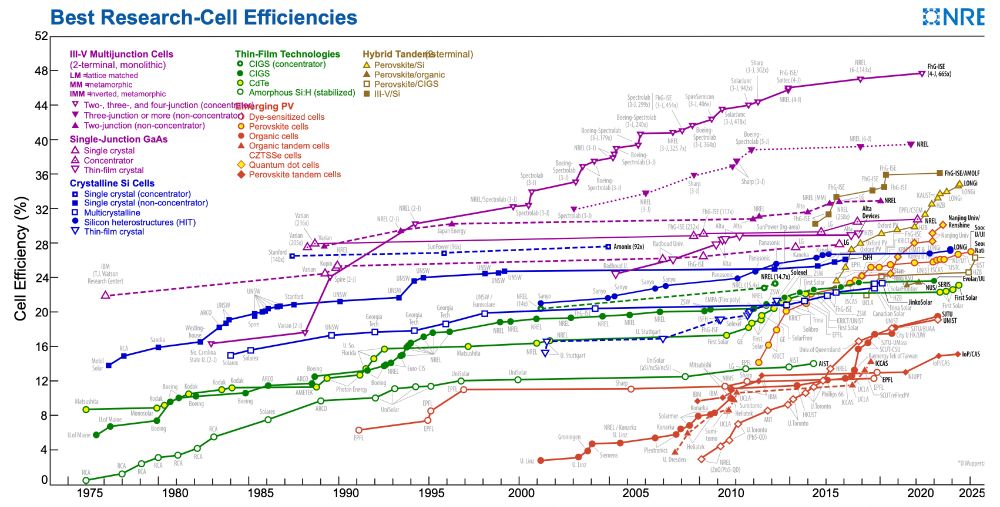
https://reionize.github.io
These ensembles can also be efficiently simulated assuming the existence of quantum-secure OWFs 💻
7/8

These ensembles can also be efficiently simulated assuming the existence of quantum-secure OWFs 💻
7/8
When the connectivity of the system is known, we show that the dynamics of any ensemble of local Hamiltonians, at any time scale, can be distinguished from a random unitary.
6/8

When the connectivity of the system is known, we show that the dynamics of any ensemble of local Hamiltonians, at any time scale, can be distinguished from a random unitary.
6/8
Under standard cryptographic assumptions, there exist Hamiltonians whose long-time dynamics perform computations that are out of reach for (& can be distinguished from) any efficient circuit 🤖
5/8

Under standard cryptographic assumptions, there exist Hamiltonians whose long-time dynamics perform computations that are out of reach for (& can be distinguished from) any efficient circuit 🤖
5/8
Not only that, determining if there exist energy-conserving PRUs for a given family of local 1D Hamiltonians is in general undecidable!
4/8

Not only that, determining if there exist energy-conserving PRUs for a given family of local 1D Hamiltonians is in general undecidable!
4/8
Excited to share a couple of works with Liang Mao, Fernando Brandão, Robert Huang, Thomas Schuster in which we explore this question!
[1] arxiv.org/abs/2510.08448
[2] arxiv.org/abs/2510.08434
1/8

Excited to share a couple of works with Liang Mao, Fernando Brandão, Robert Huang, Thomas Schuster in which we explore this question!
[1] arxiv.org/abs/2510.08448
[2] arxiv.org/abs/2510.08434
1/8

We show that the answer is no, by proving a new lower bound for the circuit depth needed for additive error designs w/ any # of ancillas
6/8

We show that the answer is no, by proving a new lower bound for the circuit depth needed for additive error designs w/ any # of ancillas
6/8
We call distinguishability in this model "measurable error"
As a bonus we give a short alternate proof of the existence of pseudorandom unitaries w/ our framework!
5/8

We call distinguishability in this model "measurable error"
As a bonus we give a short alternate proof of the existence of pseudorandom unitaries w/ our framework!
5/8
We project onto alternating local distinct subspaces on which the moments of our circuit are equal to those of fully random unitaries
4/8
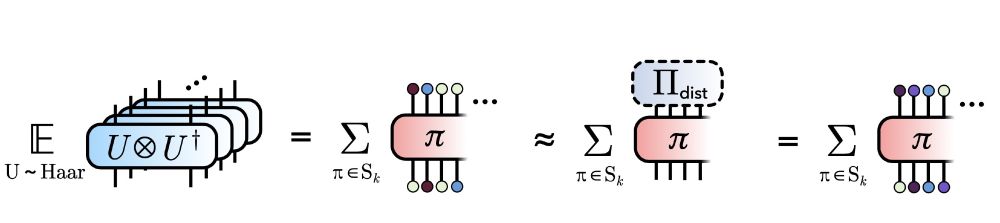
We project onto alternating local distinct subspaces on which the moments of our circuit are equal to those of fully random unitaries
4/8
We also swap permutations for *shuffling operators* based on the "nearly random" functions to bring our depth down to log k 🤠
2/8

We also swap permutations for *shuffling operators* based on the "nearly random" functions to bring our depth down to log k 🤠
2/8
In this work w/ Tommy Schuster, @RobertHuangHY, Fernando Brandão (arxiv.org/abs/2507.06216) we glue random unitary blocks w/ only random phases on log n qubits (fns on log n bits) to get designs in d = log k log log n 🧩
1/8

In this work w/ Tommy Schuster, @RobertHuangHY, Fernando Brandão (arxiv.org/abs/2507.06216) we glue random unitary blocks w/ only random phases on log n qubits (fns on log n bits) to get designs in d = log k log log n 🧩
1/8

