
Peter Kagey
@peterkagey.com
Maker, Educator, Mathematician | Assistant Professor at Cal Poly Pomona
“My interests include music, science, justice, animals, shapes, feelings” —Lisa Simpson
Creator of @oeistriangles.peterkagey.com.
“My interests include music, science, justice, animals, shapes, feelings” —Lisa Simpson
Creator of @oeistriangles.peterkagey.com.
I just heard from David that he found (and fixed!) a subtle bug in the collision checking.
It turns out that you can have two tetrahedra, T₁ and T₂ whose interiors intersect, but where T₁ (in red) does not have any edges that intersect T₂'s faces, as shown in this illustration that David sent me.
It turns out that you can have two tetrahedra, T₁ and T₂ whose interiors intersect, but where T₁ (in red) does not have any edges that intersect T₂'s faces, as shown in this illustration that David sent me.

October 28, 2025 at 5:24 PM
I just heard from David that he found (and fixed!) a subtle bug in the collision checking.
It turns out that you can have two tetrahedra, T₁ and T₂ whose interiors intersect, but where T₁ (in red) does not have any edges that intersect T₂'s faces, as shown in this illustration that David sent me.
It turns out that you can have two tetrahedra, T₁ and T₂ whose interiors intersect, but where T₁ (in red) does not have any edges that intersect T₂'s faces, as shown in this illustration that David sent me.
A Mathematica demo I made of wandering around a parameter space of the convex hull of various scalings the vertices of a icosahedron, dodecahedron, and icosidodecahedron.
Given the right parameters, we can recover all Platonic and Catalan solids with full icosahedral symmetry.
Given the right parameters, we can recover all Platonic and Catalan solids with full icosahedral symmetry.
August 21, 2025 at 4:59 PM
A Mathematica demo I made of wandering around a parameter space of the convex hull of various scalings the vertices of a icosahedron, dodecahedron, and icosidodecahedron.
Given the right parameters, we can recover all Platonic and Catalan solids with full icosahedral symmetry.
Given the right parameters, we can recover all Platonic and Catalan solids with full icosahedral symmetry.
Here's a 4-second video showing that little robot at work! ✍️🤖
August 20, 2025 at 10:43 PM
Here's a 4-second video showing that little robot at work! ✍️🤖
Made some Escher-inspired magnetic refrigerator magnets by using my AxiDraw V3 pen plotter to draw some tiles on a
magnetic vent cover.
magnetic vent cover.


August 20, 2025 at 10:41 PM
Made some Escher-inspired magnetic refrigerator magnets by using my AxiDraw V3 pen plotter to draw some tiles on a
magnetic vent cover.
magnetic vent cover.
August 18, 2025 at 8:40 PM
I learned how to use a CNC machine and wrote G-code today for the first time.


July 30, 2025 at 11:31 PM
I learned how to use a CNC machine and wrote G-code today for the first time.
Funhouse mirror icosahedron selfie made possible by @joshmillard.bsky.social

July 28, 2025 at 1:24 AM
Funhouse mirror icosahedron selfie made possible by @joshmillard.bsky.social
Am I tempted to travel to Austria just for the purpose of climbing through a 97 m³ spatial net? 😏
berliner-playequipment.com/us/referenze...
berliner-playequipment.com/us/referenze...

July 10, 2025 at 10:13 PM
Am I tempted to travel to Austria just for the purpose of climbing through a 97 m³ spatial net? 😏
berliner-playequipment.com/us/referenze...
berliner-playequipment.com/us/referenze...
Just this past month, I've been working with Pontus von Brömssen and Bert Dobbelaere on analogous problems for other space-filling polyhedra. Here are all of the ways of placing 4 cells (each 1/12 of a rhombic dodecahedron) of the rhombic pyramidal honeycomb face-to-face.
oeis.org/A385274
oeis.org/A385274
July 7, 2025 at 4:10 PM
Just this past month, I've been working with Pontus von Brömssen and Bert Dobbelaere on analogous problems for other space-filling polyhedra. Here are all of the ways of placing 4 cells (each 1/12 of a rhombic dodecahedron) of the rhombic pyramidal honeycomb face-to-face.
oeis.org/A385274
oeis.org/A385274
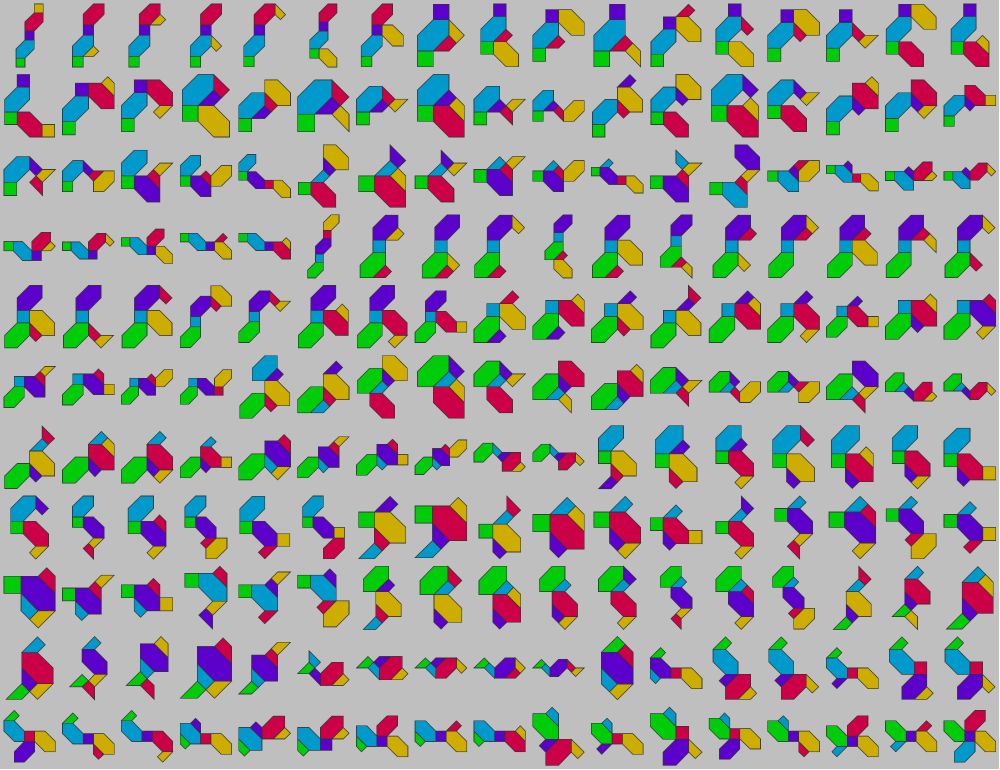
Hay 187 formas posibles que se pueden formar a partir de 5 de estas fichas.
July 3, 2025 at 10:32 PM
Hay 187 formas posibles que se pueden formar a partir de 5 de estas fichas.
Up to rotation and translation, there are 3 distinct tiles, 4 connected components of two tiles, 15 of three tiles, 47 of four tiles, and 187 components of five tiles, shown here.
Want to guess how many there are for six, seven, and eight tiles?
Want to guess how many there are for six, seven, and eight tiles?

July 3, 2025 at 10:23 PM
Up to rotation and translation, there are 3 distinct tiles, 4 connected components of two tiles, 15 of three tiles, 47 of four tiles, and 187 components of five tiles, shown here.
Want to guess how many there are for six, seven, and eight tiles?
Want to guess how many there are for six, seven, and eight tiles?
A few others (e.g. Problems 31, 79, 132) have answers or bounds now because I've worked on the problem.
For example, Problem 31 is discussed in my JIS paper with Bill Keehn, "Counting Tilings of the n × m Grid, Cylinder, and Torus."
For example, Problem 31 is discussed in my JIS paper with Bill Keehn, "Counting Tilings of the n × m Grid, Cylinder, and Torus."

June 26, 2025 at 9:21 PM
A few others (e.g. Problems 31, 79, 132) have answers or bounds now because I've worked on the problem.
For example, Problem 31 is discussed in my JIS paper with Bill Keehn, "Counting Tilings of the n × m Grid, Cylinder, and Torus."
For example, Problem 31 is discussed in my JIS paper with Bill Keehn, "Counting Tilings of the n × m Grid, Cylinder, and Torus."
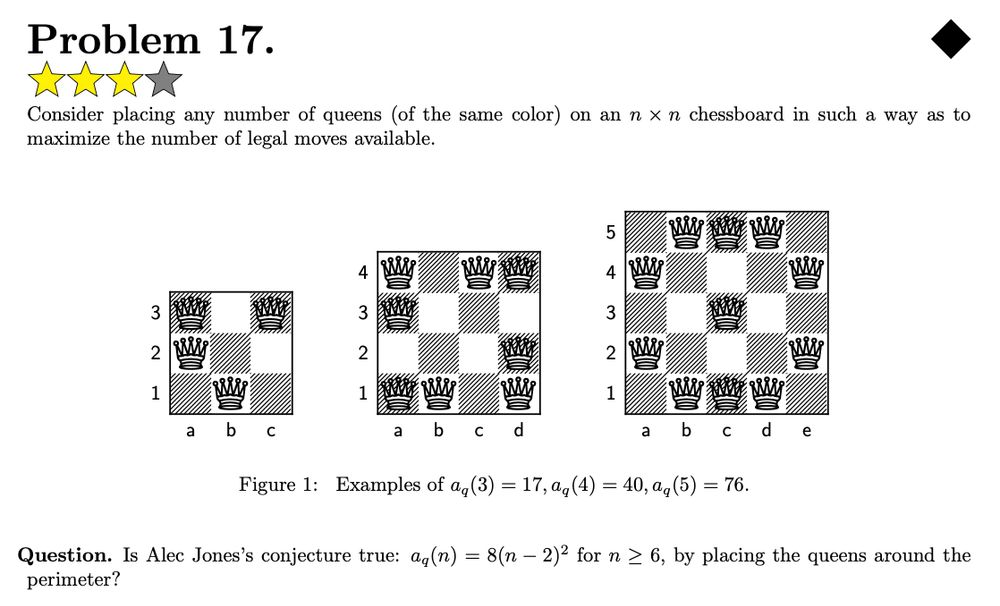
Some of the problems have answers or bounds now because I've asked about them (e.g. Problem 1, Problem 17, Problem 110)
June 26, 2025 at 9:21 PM
Some of the problems have answers or bounds now because I've asked about them (e.g. Problem 1, Problem 17, Problem 110)
Also, some of the problems, such as Problems 30, 53, 107, and 108, have solutions that were either already known or found after I wrote the problem down.

June 26, 2025 at 9:21 PM
Also, some of the problems, such as Problems 30, 53, 107, and 108, have solutions that were either already known or found after I wrote the problem down.
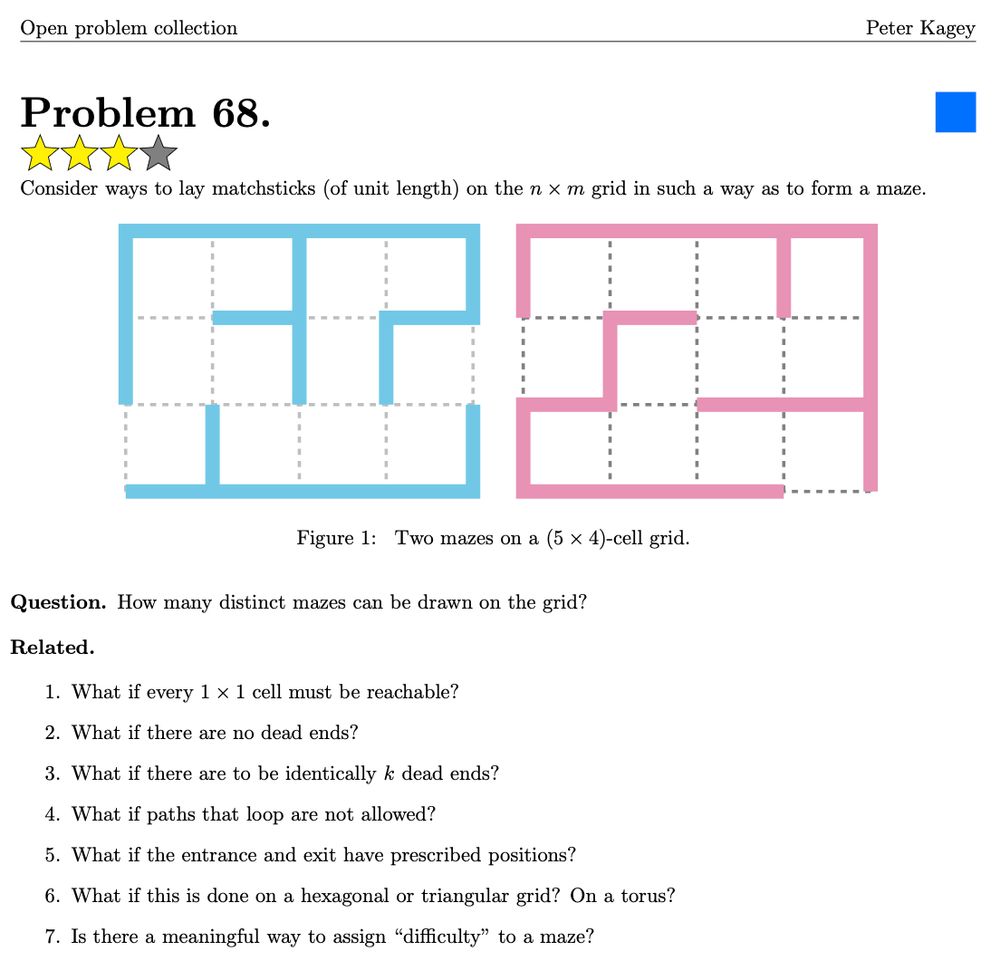
For example, the main problem in Problem 68 is definitely *not* open, although some subquestions might be.
If we close off the start/end of the maze, then we get a bijection with spanning trees on a grid graph, so counting the mazes is at most a step away from a standard result.
If we close off the start/end of the maze, then we get a bijection with spanning trees on a grid graph, so counting the mazes is at most a step away from a standard result.
June 26, 2025 at 9:21 PM
For example, the main problem in Problem 68 is definitely *not* open, although some subquestions might be.
If we close off the start/end of the maze, then we get a bijection with spanning trees on a grid graph, so counting the mazes is at most a step away from a standard result.
If we close off the start/end of the maze, then we get a bijection with spanning trees on a grid graph, so counting the mazes is at most a step away from a standard result.
This collection has 130+ questions that mathematicians might not know the answers to, but that a 10–14 year old can think deeply about (and potentially even solve!)
(Here's the specific problem that the student was working on.)
(Here's the specific problem that the student was working on.)

June 26, 2025 at 7:53 PM
This collection has 130+ questions that mathematicians might not know the answers to, but that a 10–14 year old can think deeply about (and potentially even solve!)
(Here's the specific problem that the student was working on.)
(Here's the specific problem that the student was working on.)
Last week, I was a faculty member at Camp Conway, a math camp for ~10–14 year olds outside of Los Angeles, CA.
The campers have time during their day to think about whatever they want, and I just got an email that a camper has been thinking about a problem from my "Open Problems Collection."
The campers have time during their day to think about whatever they want, and I just got an email that a camper has been thinking about a problem from my "Open Problems Collection."

June 26, 2025 at 7:53 PM
Last week, I was a faculty member at Camp Conway, a math camp for ~10–14 year olds outside of Los Angeles, CA.
The campers have time during their day to think about whatever they want, and I just got an email that a camper has been thinking about a problem from my "Open Problems Collection."
The campers have time during their day to think about whatever they want, and I just got an email that a camper has been thinking about a problem from my "Open Problems Collection."
We played GoL with wraparound—so I showed them why we call this a torus too!
June 18, 2025 at 10:23 PM
We played GoL with wraparound—so I showed them why we call this a torus too!
I'm a faculty member at "Camp Conway" this week and I was asked to give a talk during the morning session.
Of course, every student who goes to Camp Conway should come home knowing a little bit about Conway's Game of Life, so I made Conway's GoL starting with initial conditions of Conway.
Of course, every student who goes to Camp Conway should come home knowing a little bit about Conway's Game of Life, so I made Conway's GoL starting with initial conditions of Conway.
June 18, 2025 at 10:23 PM
I'm a faculty member at "Camp Conway" this week and I was asked to give a talk during the morning session.
Of course, every student who goes to Camp Conway should come home knowing a little bit about Conway's Game of Life, so I made Conway's GoL starting with initial conditions of Conway.
Of course, every student who goes to Camp Conway should come home knowing a little bit about Conway's Game of Life, so I made Conway's GoL starting with initial conditions of Conway.

June 4, 2025 at 5:34 PM
And precisely 500 ways of choosing six of them!

May 28, 2025 at 11:47 PM
And precisely 500 ways of choosing six of them!
And 123 ways of choosing five of them.

May 28, 2025 at 11:47 PM
And 123 ways of choosing five of them.
There are 30 ways of choosing connected components of four of these Highland Park, CA driveway tiles up to rotation, reflection, and translation.

May 28, 2025 at 11:47 PM
There are 30 ways of choosing connected components of four of these Highland Park, CA driveway tiles up to rotation, reflection, and translation.
Next step: buy a 3D printer and print a puzzle!
May 25, 2025 at 7:28 PM
Next step: buy a 3D printer and print a puzzle!


