muratkocaoglu.com/CausalML/
github.com/CausalML-Lab
muratkocaoglu.com/CausalML/
github.com/CausalML-Lab
Led by my PhD students Zihan Zhou and Qasim Elahi.
Paper link:
openreview.net/forum?id=RfS...
Follow us for more updates from the #CausalML Lab!

Led by my PhD students Zihan Zhou and Qasim Elahi.
Paper link:
openreview.net/forum?id=RfS...
Follow us for more updates from the #CausalML Lab!
Green at the bottom is ours vs. some baselines.
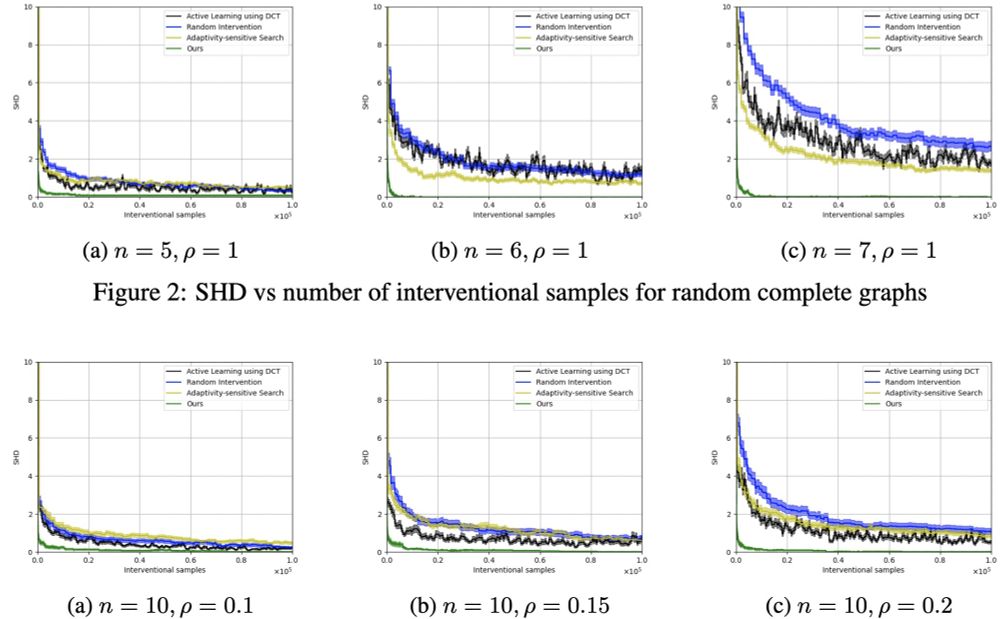
Green at the bottom is ours vs. some baselines.
Instead of keeping track of all causal DAGs, can we keep track of a compact set of subgraphs?
Instead of keeping track of all causal DAGs, can we keep track of a compact set of subgraphs?
Led by my PhD student Qasim Elahi. Joint work with my colleague Mahsa Ghasemi.
Paper link:
openreview.net/forum?id=uM3...
Follow us for more updates from the #CausalML Lab!

Led by my PhD student Qasim Elahi. Joint work with my colleague Mahsa Ghasemi.
Paper link:
openreview.net/forum?id=uM3...
Follow us for more updates from the #CausalML Lab!

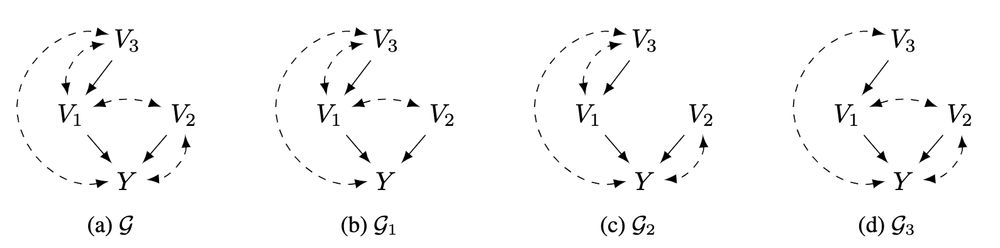
We propose an interventional causal discovery algorithm that takes advantage of this observation.
We propose an interventional causal discovery algorithm that takes advantage of this observation.
Do we need to know all unobserved confounders to learn all POMISes? Or can we get away without knowing some?
This is not obvious.
Do we need to know all unobserved confounders to learn all POMISes? Or can we get away without knowing some?
This is not obvious.

