
interested in intelligence
of a random quadratic 2D polynomial map
~50 million points per frame — rendered in C++
sound: mystery or misery? — vegyn
of a random quadratic 2D polynomial map
~50 million points per frame — rendered in C++
sound: mystery or misery? — vegyn
There’s more evidence for that perspective:
x.com/hippopedoid/...
There’s more evidence for that perspective:
x.com/hippopedoid/...
The (pink) image is colored by integer magnitude (bright = large). Some trajectories hint at sequences, but no formal classification was made.
johnhw.github.io/umap_primes/...
The (pink) image is colored by integer magnitude (bright = large). Some trajectories hint at sequences, but no formal classification was made.
johnhw.github.io/umap_primes/...
Written around 300 BC in ancient Greece, this edition is its first English translation (1570). It remained a core math textbook well into the 20th century.

Written around 300 BC in ancient Greece, this edition is its first English translation (1570). It remained a core math textbook well into the 20th century.
go.epfl.ch/smooth_rolling_knots
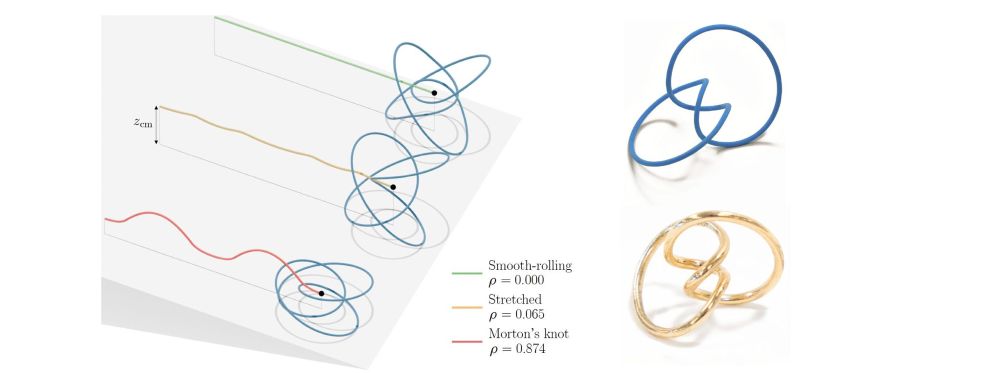
go.epfl.ch/smooth_rolling_knots
Smooth-rolling objects require virtually no force to start moving – even with low friction, they roll.
Smooth-rolling objects require virtually no force to start moving – even with low friction, they roll.
We created knots with this property by combining Morton’s knots with Two-Disk Rollers.
We created knots with this property by combining Morton’s knots with Two-Disk Rollers.
Your Repulsive Curves are actually what got me working on knots in the first place. :)
Your Repulsive Curves are actually what got me working on knots in the first place. :)
1 → [0, 0, 0, …]
2 → [1, 0, 0, …]
3 → [0, 1, 0, …]
6 (2×3) → [1, 1, 0, …]
30 (2×3×5) → [1, 1, 1, 0, …]
Each bit = “is divisible by the n-th prime?”
1 → [0, 0, 0, …]
2 → [1, 0, 0, …]
3 → [0, 1, 0, …]
6 (2×3) → [1, 1, 0, …]
30 (2×3×5) → [1, 1, 1, 0, …]
Each bit = “is divisible by the n-th prime?”


