Smacked a time or two with the autism stick, don't get offended if I insist on calling your foot-powered digging implement a spade.
This gives only one solution,
a = 6
b = 9
c = -3
d = -25
e = 5
f = -1
g = -7
h = -2
i = 8 ✅

This gives only one solution,
a = 6
b = 9
c = -3
d = -25
e = 5
f = -1
g = -7
h = -2
i = 8 ✅
applied to the two number-solutions we already had gives us a grand total of 32 possibilities. 👍
Now we just have to find put which fulfil the grey-box condition.
4/
applied to the two number-solutions we already had gives us a grand total of 32 possibilities. 👍
Now we just have to find put which fulfil the grey-box condition.
4/
Let's label our cells as
a b c F
d e f T
g h i T
T F T
c = not xor(a, b)
f = xor(d, e)
g = xor(a, d)
h = not xor(b, e)
i = xor(not xor(a, b), xor(d, e))
So we only need to consider the independent variables a, b, d, e.
3/
Let's label our cells as
a b c F
d e f T
g h i T
T F T
c = not xor(a, b)
f = xor(d, e)
g = xor(a, d)
h = not xor(b, e)
i = xor(not xor(a, b), xor(d, e))
So we only need to consider the independent variables a, b, d, e.
3/
We can solve this as a parity problem, encoding +ve as True and -ve as False.
If we look at possible combinations,
T • T = T
T • F = F
F • T = F
F • F = T
which matches the XOR operator 👍
2/
We can solve this as a parity problem, encoding +ve as True and -ve as False.
If we look at possible combinations,
T • T = T
T • F = F
F • T = F
F • F = T
which matches the XOR operator 👍
2/
1/
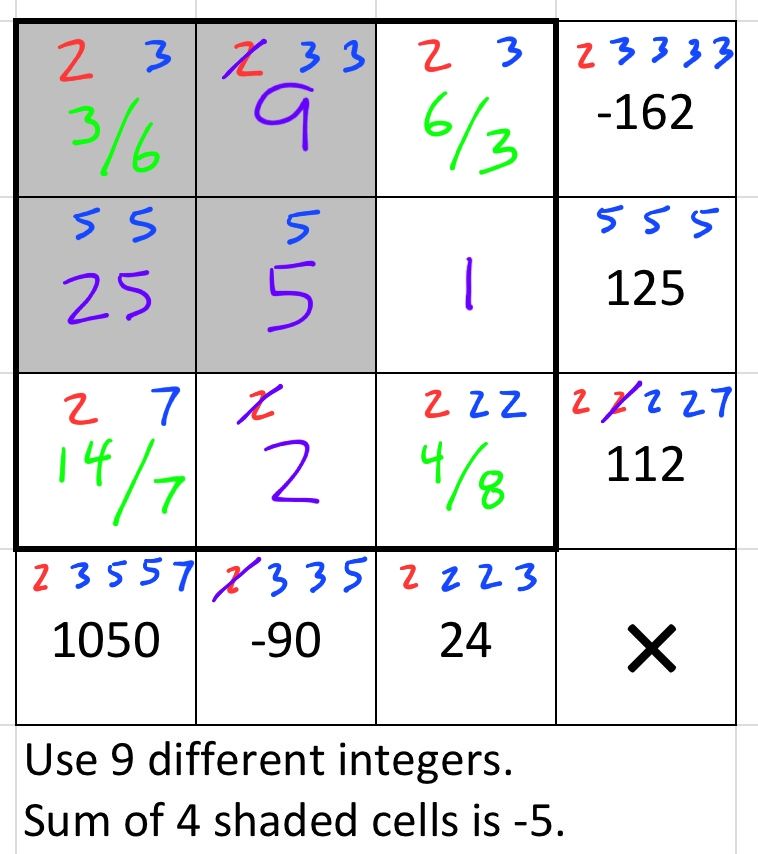
1/
1/12 + 1/20 + 1/30 + 1/72 + 1/90 + 1/110 + 1/156 + 1/182
+ 1/210 + 1/240 + 1/272 + 1/306 + 1/342 + 1/380 + 1/420
+ 1/462 + 1/600 + 1/650 + 1/702 + 1/756 + 1/812 + 1/870
+ 1/930 + 1/992 + 1/1056
= 1/4 🥳
1/12 + 1/20 + 1/30 + 1/72 + 1/90 + 1/110 + 1/156 + 1/182
+ 1/210 + 1/240 + 1/272 + 1/306 + 1/342 + 1/380 + 1/420
+ 1/462 + 1/600 + 1/650 + 1/702 + 1/756 + 1/812 + 1/870
+ 1/930 + 1/992 + 1/1056
= 1/4 🥳
What would *really* help would be a better algorithm; but I can't picture what that would look like, I think I've got this one pretty well cinched down tight. 🤔
4/
What would *really* help would be a better algorithm; but I can't picture what that would look like, I think I've got this one pretty well cinched down tight. 🤔
4/
I could run the basic solver until my state-table is ie a million entries, then split it into hundred-entry chunks and restart each on 10,000 different machines,
3/
I could run the basic solver until my state-table is ie a million entries, then split it into hundred-entry chunks and restart each on 10,000 different machines,
3/
2/
2/
That ran for 11 minutes and got me up to 188 solutions before locking my machine (Python using 28.3 GB of RAM) 😂.
1/
That ran for 11 minutes and got me up to 188 solutions before locking my machine (Python using 28.3 GB of RAM) 😂.
1/
Unfortunately Trump is also the law-breaking-est president, and surrounded by idiot goons happy to break the law for him.
Unfortunately Trump is also the law-breaking-est president, and surrounded by idiot goons happy to break the law for him.

