
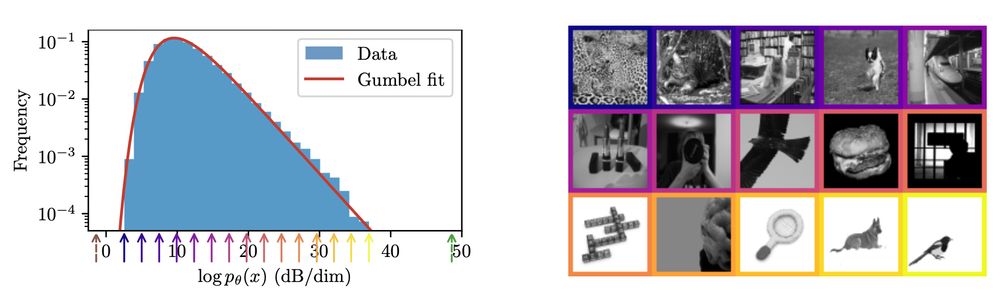

In addition to computing cross-entropy/NLL, we show *strong* generalization: models trained on *disjoint* subsets of the data predict the *same* probabilities if the training set is large enough!

In addition to computing cross-entropy/NLL, we show *strong* generalization: models trained on *disjoint* subsets of the data predict the *same* probabilities if the training set is large enough!


Inspired by diffusion models, we learn the energy of both clean and noisy images along a diffusion. It is optimized via a sum of two score matching objectives, which constrain its derivatives with both the image (space) and the noise level (time).

Inspired by diffusion models, we learn the energy of both clean and noisy images along a diffusion. It is optimized via a sum of two score matching objectives, which constrain its derivatives with both the image (space) and the noise level (time).
- what we should do to improve/replace these huge conferences
- replica method and other statphys-inspired high-dim probability (finally trying to understand what the fuss is about)
- textbooks that have been foundational/transformative for your work
- what we should do to improve/replace these huge conferences
- replica method and other statphys-inspired high-dim probability (finally trying to understand what the fuss is about)
- textbooks that have been foundational/transformative for your work

