
RL Theory Lecture Notes: https://arxiv.org/abs/2312.16730
Many interesting questions: What are the minimal conditions for RL success (maybe a more semantic notion of coverage)? Do other algos/interventions secretly have coverage-based interpretations?
Many interesting questions: What are the minimal conditions for RL success (maybe a more semantic notion of coverage)? Do other algos/interventions secretly have coverage-based interpretations?


1. Vanilla SGD can have poor coverage; gradient normalization (a-la Adam) fixes this
2. Test-time training (SGD on tokens during generation) provably improves coverage

1. Vanilla SGD can have poor coverage; gradient normalization (a-la Adam) fixes this
2. Test-time training (SGD on tokens during generation) provably improves coverage
1. New generalization analysis for next-token prediction/maximum likelihood for general function classes, in the vein of stat. learning.
2. SGD in the one-pass regime for overparameterized autoregressive linear models
1. New generalization analysis for next-token prediction/maximum likelihood for general function classes, in the vein of stat. learning.
2. SGD in the one-pass regime for overparameterized autoregressive linear models
Neat consequence: Coverage generalizes faster as we go further into tail (corresponding to more test-time compute)

Neat consequence: Coverage generalizes faster as we go further into tail (corresponding to more test-time compute)
- Cross-entropy decreases throughout training.
- Coverage improves to a point, but begins to drop as the model learns a spurious shortcut.
- BoN performance follows trend of coverage, not CE (increasing initially, dropping as shortcut is learned).

- Cross-entropy decreases throughout training.
- Coverage improves to a point, but begins to drop as the model learns a spurious shortcut.
- BoN performance follows trend of coverage, not CE (increasing initially, dropping as shortcut is learned).
1) Next-token prediction (more generally, MLE) provably learns a model w/ good coverage, inheriting the training corpus’ coverage over tasks of interest.
2) Coverage generalizes *faster* than cross-entropy itself, and consequently can be more predictive.

1) Next-token prediction (more generally, MLE) provably learns a model w/ good coverage, inheriting the training corpus’ coverage over tasks of interest.
2) Coverage generalizes *faster* than cross-entropy itself, and consequently can be more predictive.
Empirically, some notion of coverage also seems necessary for current RL methods (eg arxiv.org/abs/2504.13837)
Empirically, some notion of coverage also seems necessary for current RL methods (eg arxiv.org/abs/2504.13837)
N controls how far into tail we go, and roughly corresponds to test-time compute/RL effort. For downstream performance, the tail is what matters.
N controls how far into tail we go, and roughly corresponds to test-time compute/RL effort. For downstream performance, the tail is what matters.
Cov_N = P_{π}[π(y|x)/\hat{π}(y|x) ≥ N],
(π is pre-training dist, \hat{π} is pre-trained model, N is a param)

Cov_N = P_{π}[π(y|x)/\hat{π}(y|x) ≥ N],
(π is pre-training dist, \hat{π} is pre-trained model, N is a param)
Concretely, what metrics of the pre-trained model can we link to downstream success?
Concretely, what metrics of the pre-trained model can we link to downstream success?

Paper: www.arxiv.org/abs/2510.15020
Thread below.

Paper: www.arxiv.org/abs/2510.15020
Thread below.
1. Vanilla SGD can have poor coverage; gradient normalization (a-la Adam) fixes this
2. Test-time training (SGD on tokens during generation) provably improves coverage

1. Vanilla SGD can have poor coverage; gradient normalization (a-la Adam) fixes this
2. Test-time training (SGD on tokens during generation) provably improves coverage

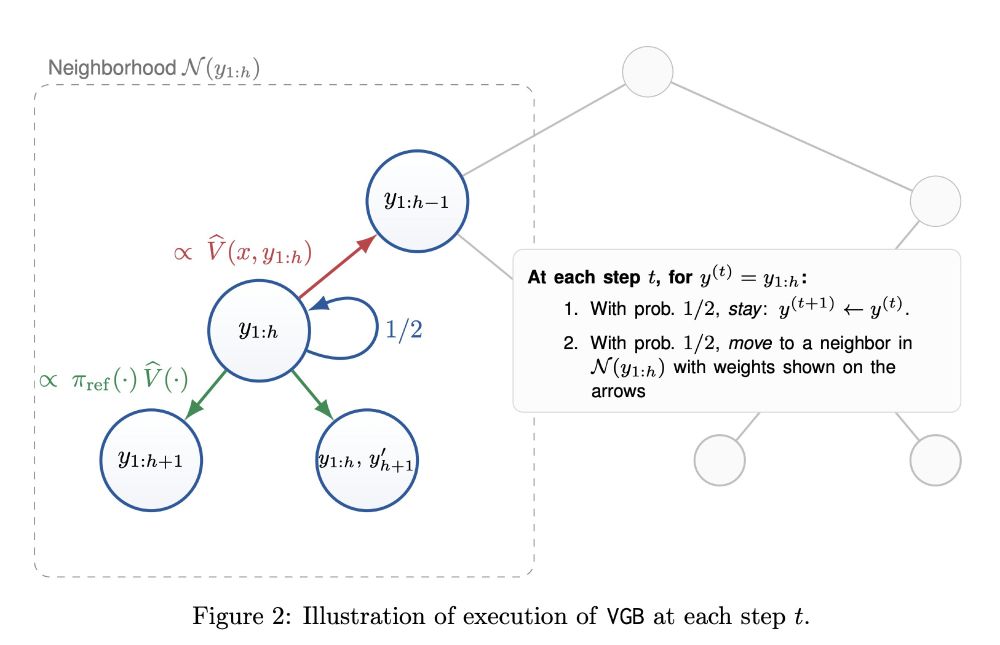
- As long as you have exact/verifiable outcome rewards, always converges to optimal distribution.
- Runtime depends on process verifier quality, gracefully degrading as quality gets worse.

- As long as you have exact/verifiable outcome rewards, always converges to optimal distribution.
- Runtime depends on process verifier quality, gracefully degrading as quality gets worse.
from TCS (used to prove equivalence of apx. counting & sampling for self-reducible problems), linking test-time RL/alignment with discrete sampling theory. We are super excited about this connection.

from TCS (used to prove equivalence of apx. counting & sampling for self-reducible problems), linking test-time RL/alignment with discrete sampling theory. We are super excited about this connection.

Short thread below.
Short thread below.

