
X: @ChrisWLynn
Lab: lynnlab.yale.edu/
“Physics at its best is a point of view for understanding the totality of man and the Universe.”

“Physics at its best is a point of view for understanding the totality of man and the Universe.”
For example, in models of kinesin (a motor protein that ships cargo inside your cells), we can derive simplified dynamics without losing any irreversibility.
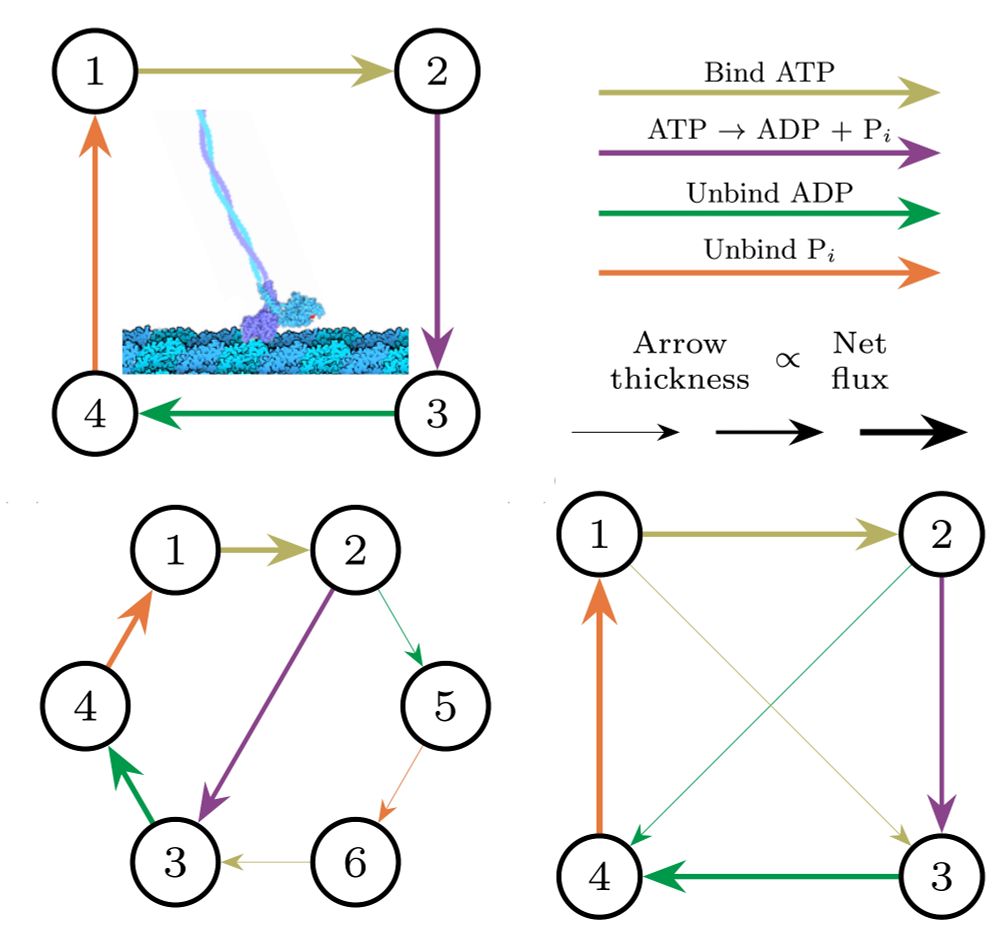
For example, in models of kinesin (a motor protein that ships cargo inside your cells), we can derive simplified dynamics without losing any irreversibility.
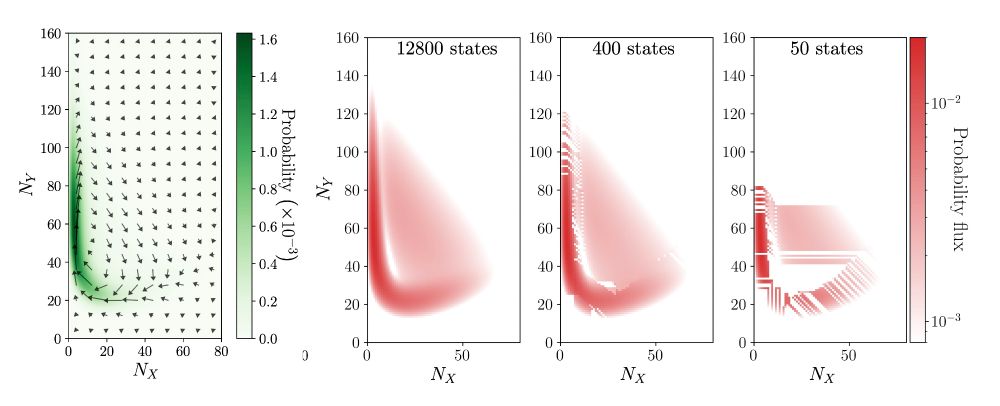
Under coarse-graining, the apparent irreversibility can only decrease.
This means that -- at every level of description -- there's a unique coarse-graining with maximum irreversibility.
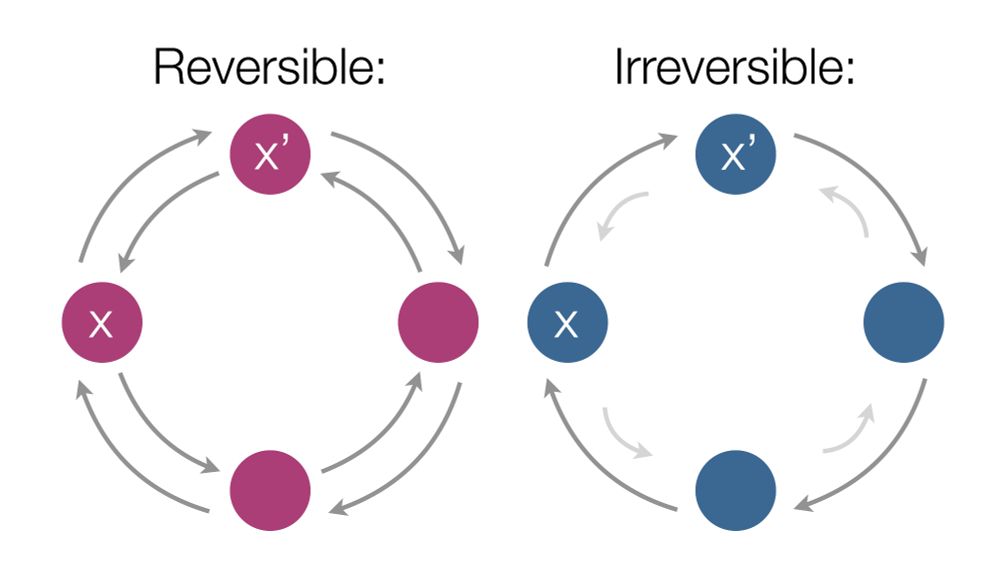
Under coarse-graining, the apparent irreversibility can only decrease.
This means that -- at every level of description -- there's a unique coarse-graining with maximum irreversibility.
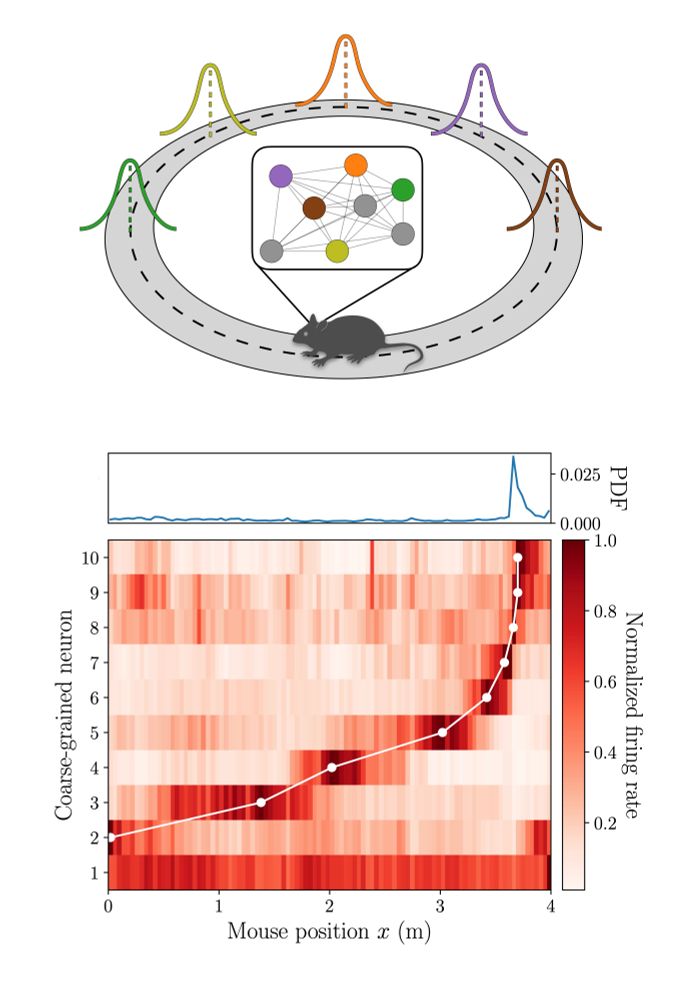
Led by @qiweiyu.bsky.social and @mleighton.bsky.social, we study how coarse-graining can help to bridge this gap 👇🧵
arxiv.org/abs/2506.01909
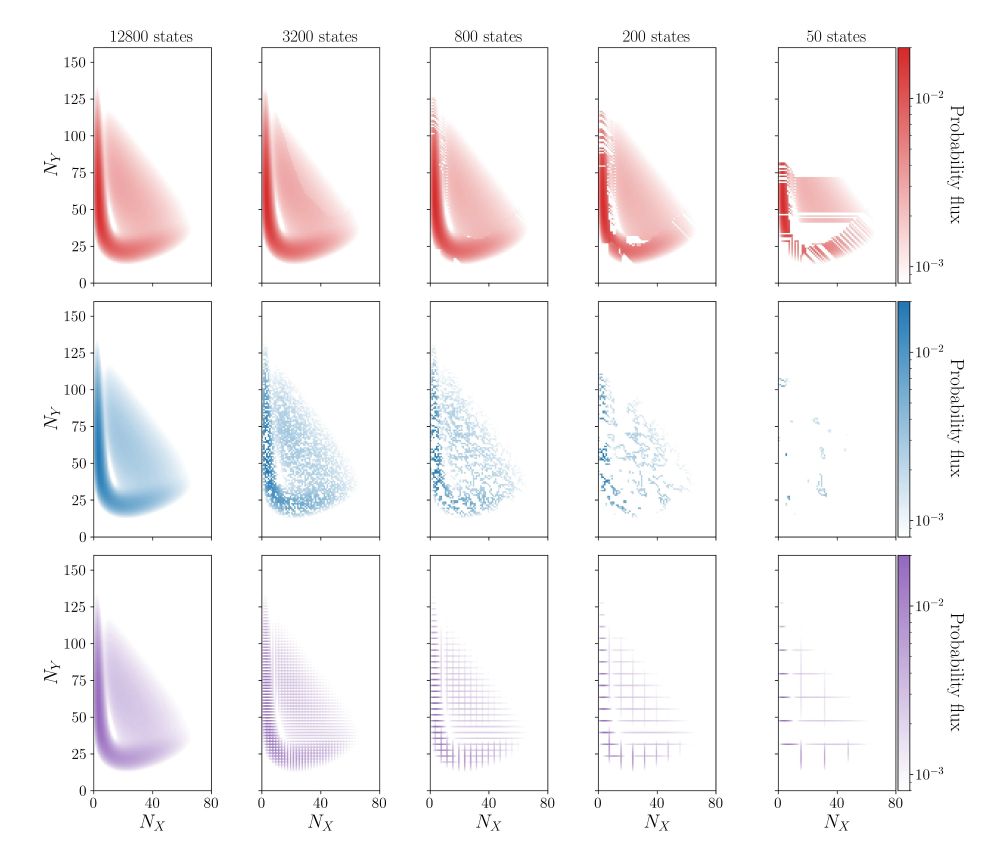
Led by @qiweiyu.bsky.social and @mleighton.bsky.social, we study how coarse-graining can help to bridge this gap 👇🧵
arxiv.org/abs/2506.01909


For example, in models of kinesin (a motor protein that ships cargo inside your cells), we can derive simplified dynamics without losing any irreversibility.

For example, in models of kinesin (a motor protein that ships cargo inside your cells), we can derive simplified dynamics without losing any irreversibility.
Under coarse-graining, the apparent irreversibility can only decrease.
This means that -- at every level of description -- there's a unique coarse-graining with maximum irreversibility.

Under coarse-graining, the apparent irreversibility can only decrease.
This means that -- at every level of description -- there's a unique coarse-graining with maximum irreversibility.
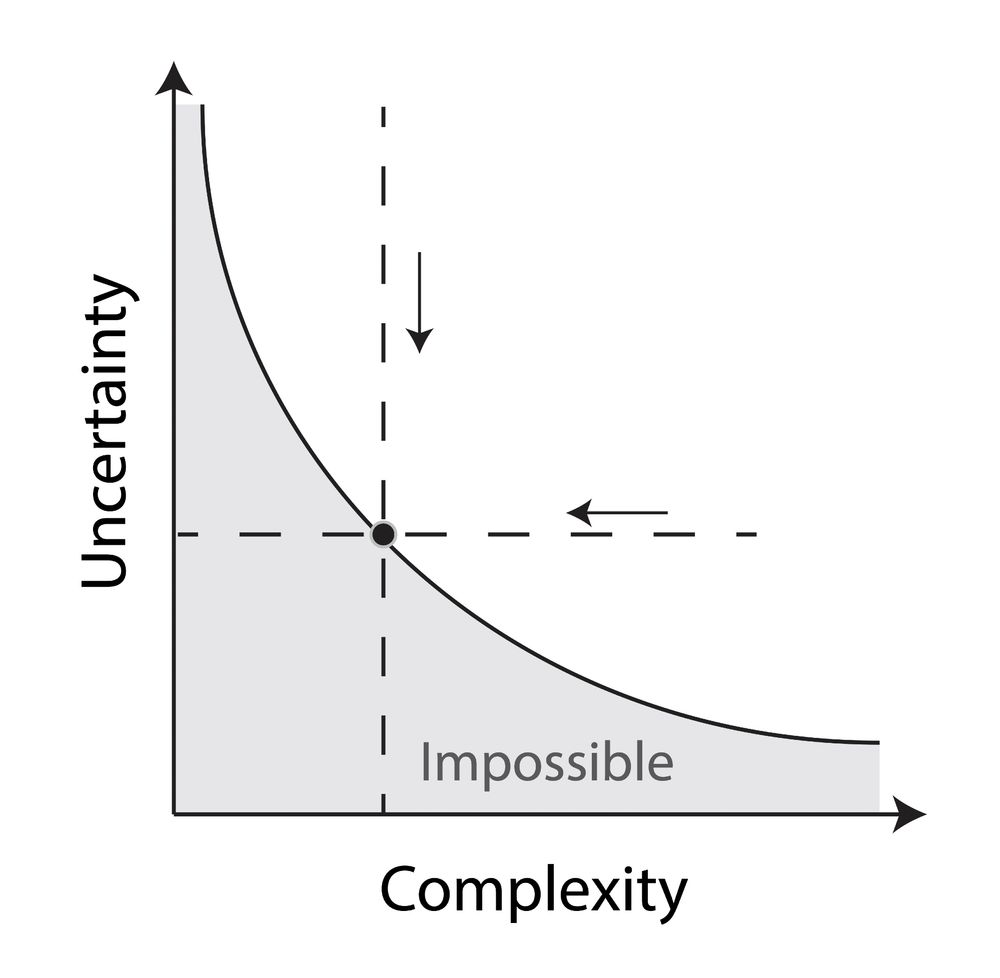
This "minimax entropy" principle was proposed 25 years ago but remains largely unexplored
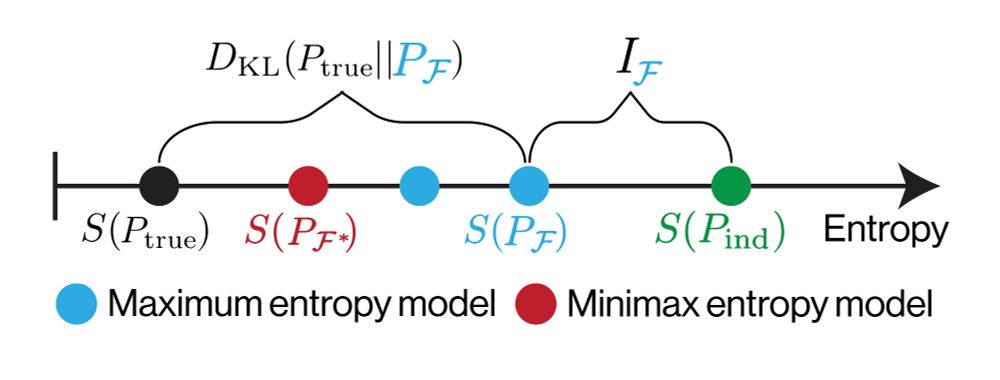
This "minimax entropy" principle was proposed 25 years ago but remains largely unexplored
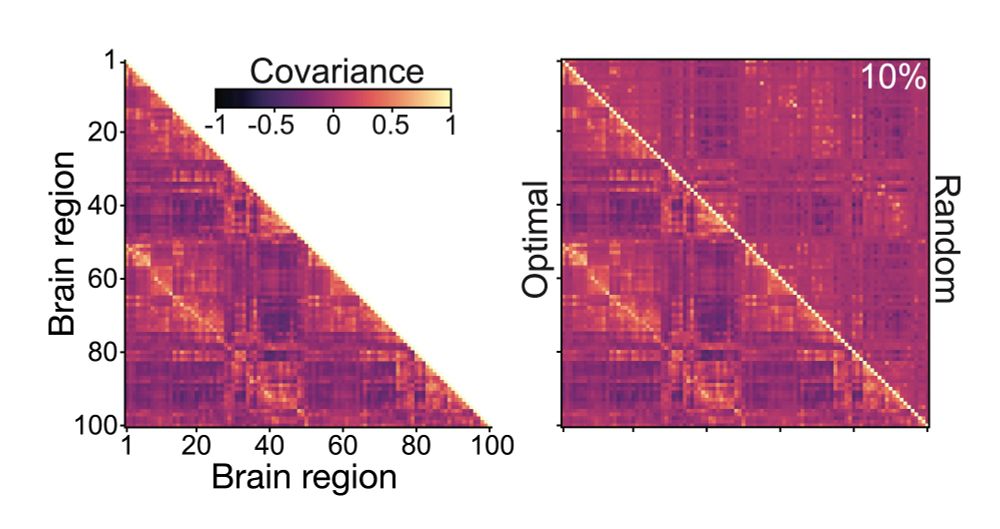
An answer lies in the "minimax entropy" principle 👇
arxiv.org/abs/2505.01607
An answer lies in the "minimax entropy" principle 👇
arxiv.org/abs/2505.01607
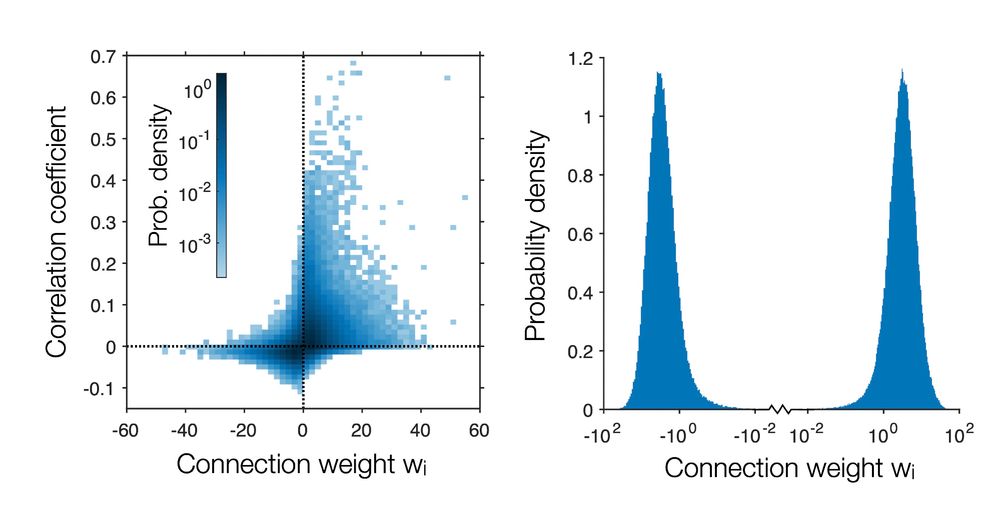
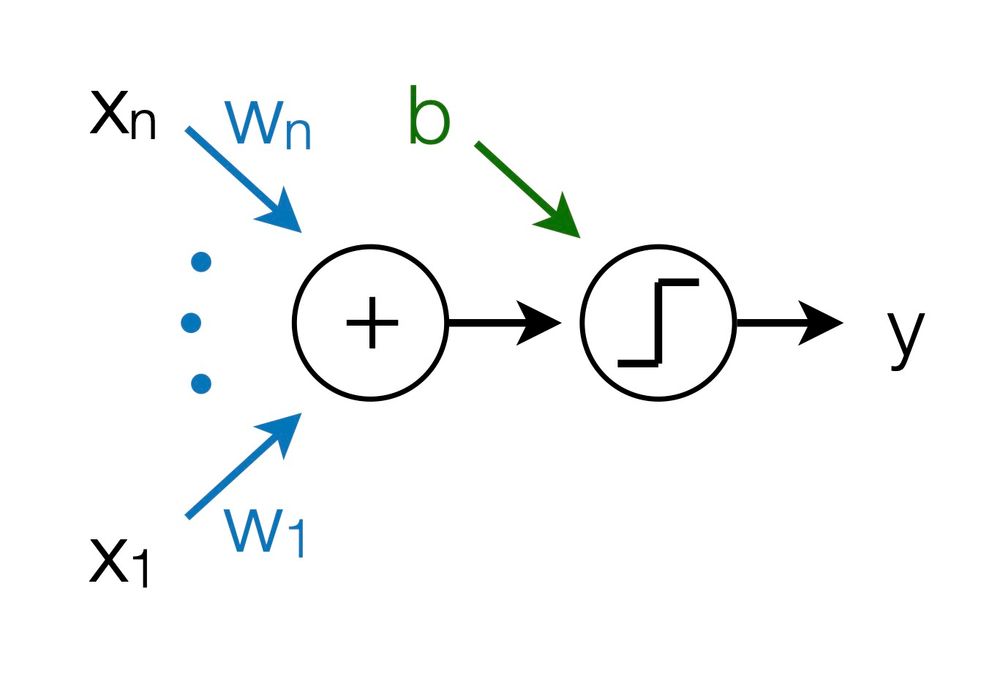

1. Direct dependencies on inputs (as in artificial neurons)
2. Indirect dependencies (which require interactions between inputs)
3. Inherent stochasticity (which doesn't depend on inputs)

1. Direct dependencies on inputs (as in artificial neurons)
2. Indirect dependencies (which require interactions between inputs)
3. Inherent stochasticity (which doesn't depend on inputs)
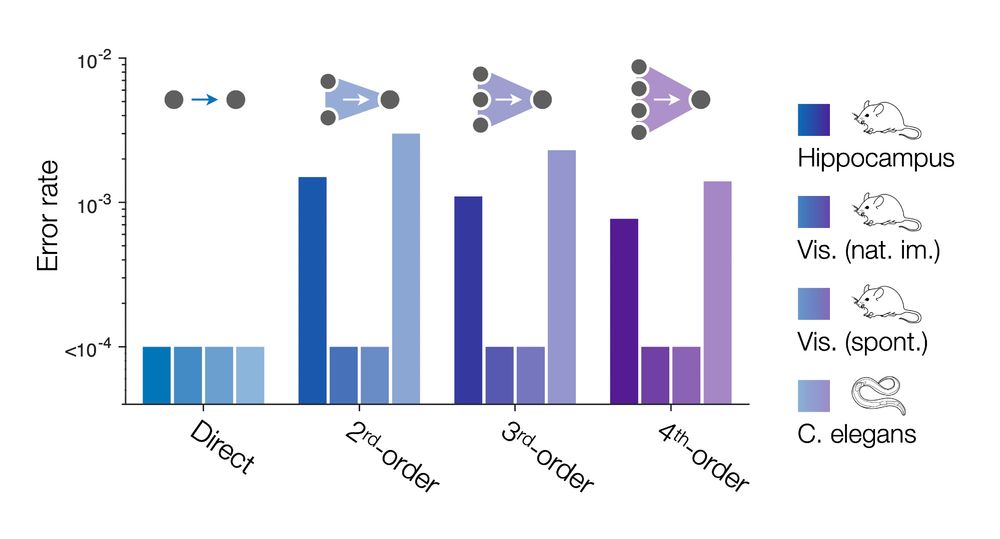
We systematically test this assumption 👇 arxiv.org/abs/2504.08637

We systematically test this assumption 👇 arxiv.org/abs/2504.08637

