
https://almostsuremath.com
Also on YouTube: https://www.youtube.com/@almostsure

It does for commutative & free products, as products of initial algebras.
Doesn't look like it does for boolean independence. Not as until algebras though.
Maybe as non-initial ones
It does for commutative & free products, as products of initial algebras.
Doesn't look like it does for boolean independence. Not as until algebras though.
Maybe as non-initial ones
Would the same thing with normal tyres result in loss of control, or was this a result of reckless driving?
Would the same thing with normal tyres result in loss of control, or was this a result of reckless driving?
Maybe there is a more natural way of fitting martingales.
bsky.app/profile/almo...
X(mu,t)->1-X(1-mu,t).
It is for individual times, as it matches Dirichlet distribution, but probably not for the entire paths wrt t. Which is disappointing. Maybe it can be modified?
X(μ,t) ~ Beta(μ(1-t)/t, (1-μ)(1-t)/t)
The (1-t)/t scaling is so that on range 0<t<1 we cover entire set of Beta distributions.
For each t, X(μ_{i+1},t)-X(μ_i,t) have Dirichlet distribution.
Maybe there is a more natural way of fitting martingales.
bsky.app/profile/almo...
And, gamma(1) process scaled to hit 1 at time 1 (time parameter mu to compare). Corresponds to t=0.5 in the surface plot. You can see its dominated by a few large jumps.
gamma(40) process is shown in the 3rd plot, corresponds with t=0.024

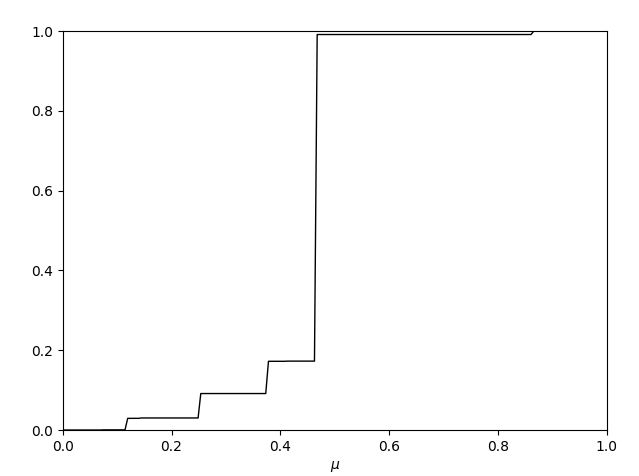

And, gamma(1) process scaled to hit 1 at time 1 (time parameter mu to compare). Corresponds to t=0.5 in the surface plot. You can see its dominated by a few large jumps.
gamma(40) process is shown in the 3rd plot, corresponds with t=0.024

