Here we provide CountDown as a ICL task.
Interestingly, in R1-14B, our interventions lead to partial success - the LM fails self-verification but then self-corrects itself.
7/n

Here we provide CountDown as a ICL task.
Interestingly, in R1-14B, our interventions lead to partial success - the LM fails self-verification but then self-corrects itself.
7/n
We use “interlayer communication channels” to rank how much each head (OV circuit) aligns with the “receptive fields” of verification-related MLP weights.
Disable *three* heads → disables self-verif. and deactivates verif.-MLP weights.
6/n
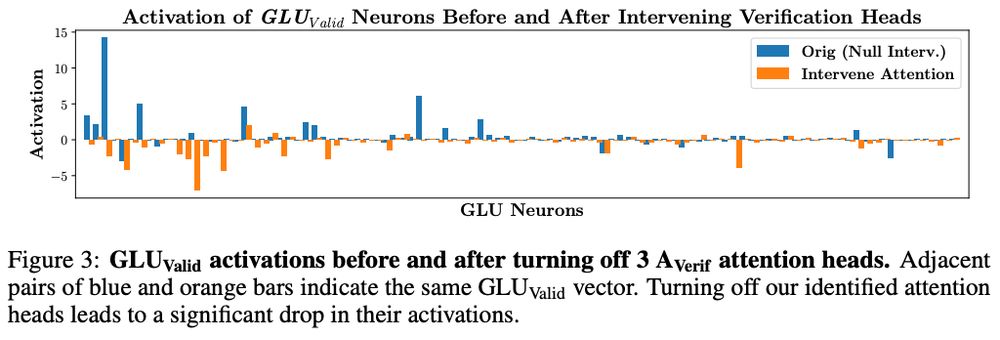
We use “interlayer communication channels” to rank how much each head (OV circuit) aligns with the “receptive fields” of verification-related MLP weights.
Disable *three* heads → disables self-verif. and deactivates verif.-MLP weights.
6/n
5/n
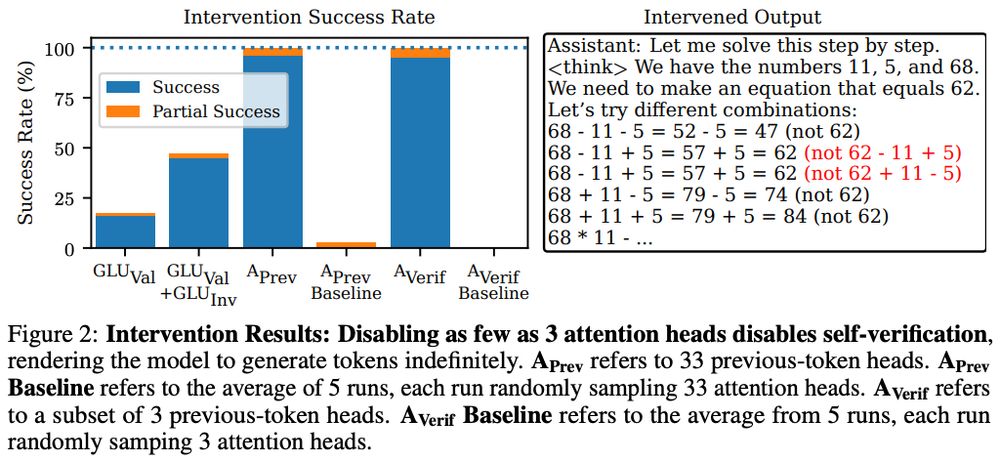
5/n
Interestingly, we often see Eng. tokens for "valid direction" and Chinese tokens for "invalid direction".
4/n

Interestingly, we often see Eng. tokens for "valid direction" and Chinese tokens for "invalid direction".
4/n
3/n
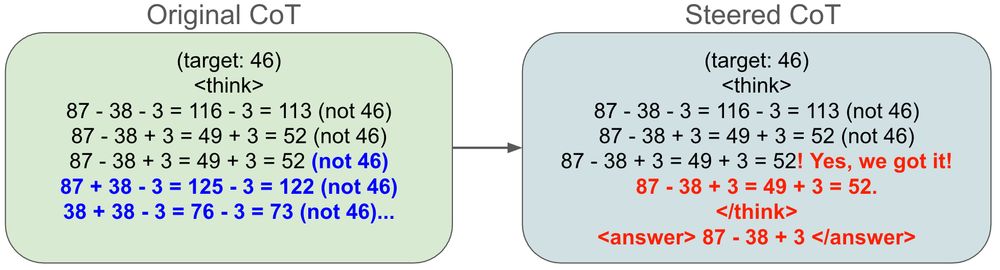
3/n
Case study: Let’s study self-verification!
Setup: We train Qwen-3B on CountDown until mode collapse, resulting in nicely structured CoT that’s easy to parse+analyze
2/n

Case study: Let’s study self-verification!
Setup: We train Qwen-3B on CountDown until mode collapse, resulting in nicely structured CoT that’s easy to parse+analyze
2/n
How do reasoning models verify their own CoT?
We reverse-engineer LMs and find critical components and subspaces needed for self-verification!
1/n

How do reasoning models verify their own CoT?
We reverse-engineer LMs and find critical components and subspaces needed for self-verification!
1/n
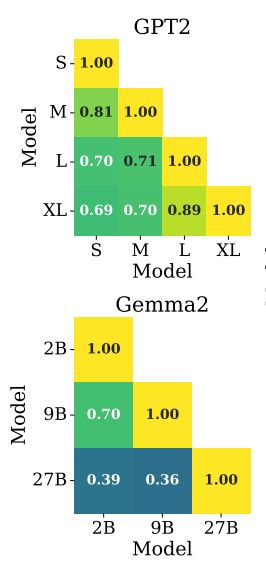


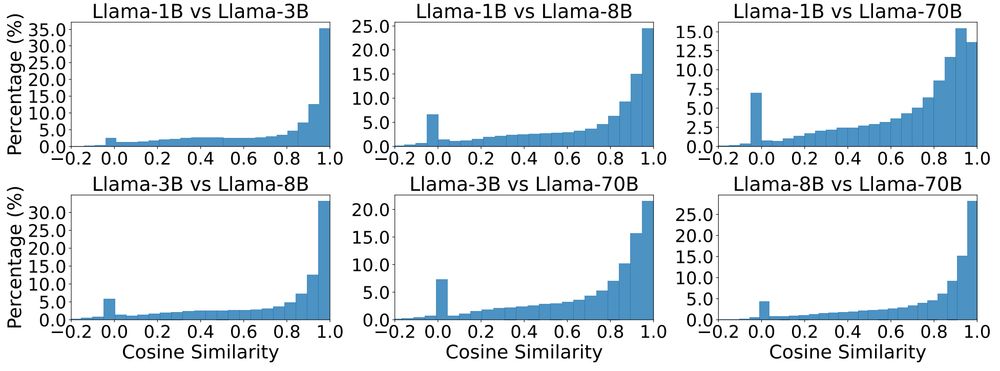
Global: how similar are the distance matrices of embeddings across LMs? We can check with Pearson correlation between distance matrices: high correlation indicates similar relative orientations of token embeddings, which is what we find
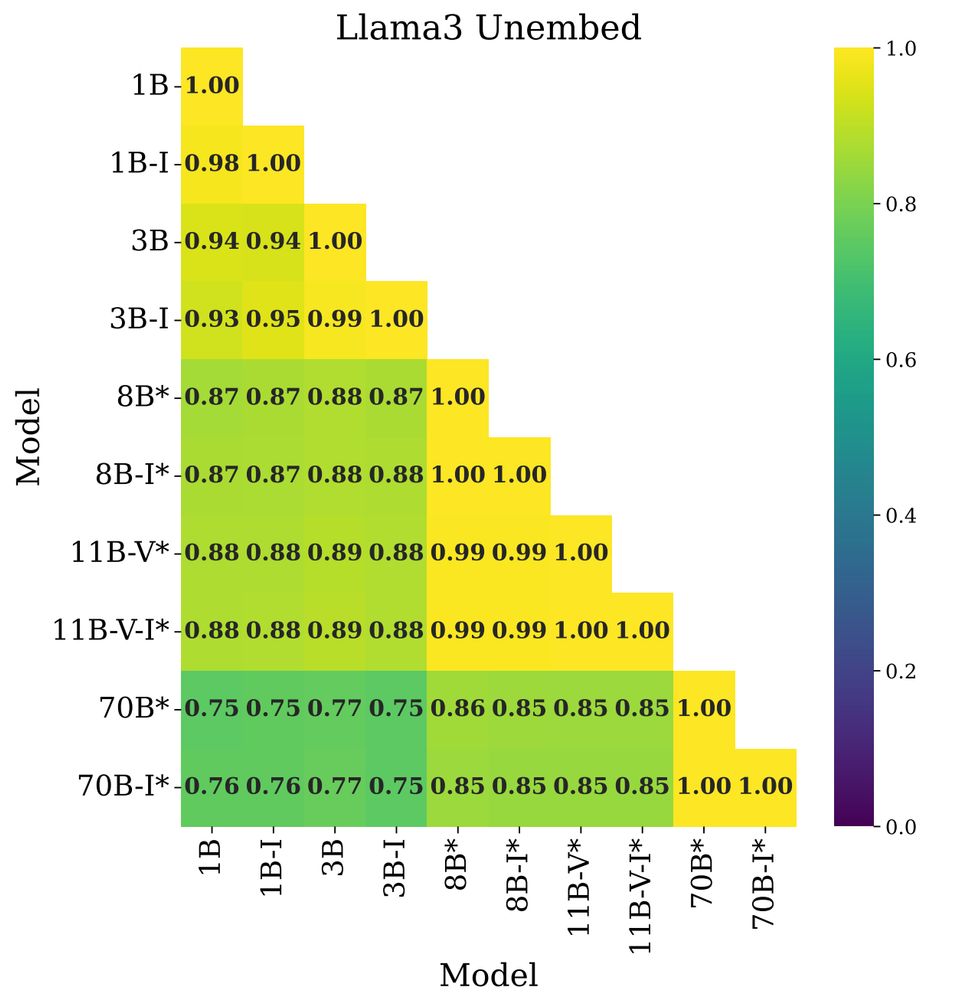
Global: how similar are the distance matrices of embeddings across LMs? We can check with Pearson correlation between distance matrices: high correlation indicates similar relative orientations of token embeddings, which is what we find

ajyl.github.io/2025/02/16/s...
5/N

ajyl.github.io/2025/02/16/s...
5/N
github.com/ARBORproject...
github.com/ARBORproject...
8/N

8/N
7/N

7/N
6/N

6/N
We make an in-context task with a new ordering of days (Mon,Thurs,Sun,Wed…): The orig. semantic prior shows up in first principal components & in-context reps in latter ones! The two co-exist.
5/N

We make an in-context task with a new ordering of days (Mon,Thurs,Sun,Wed…): The orig. semantic prior shows up in first principal components & in-context reps in latter ones! The two co-exist.
5/N
These rings can also be formed in-context!
4/N

These rings can also be formed in-context!
4/N
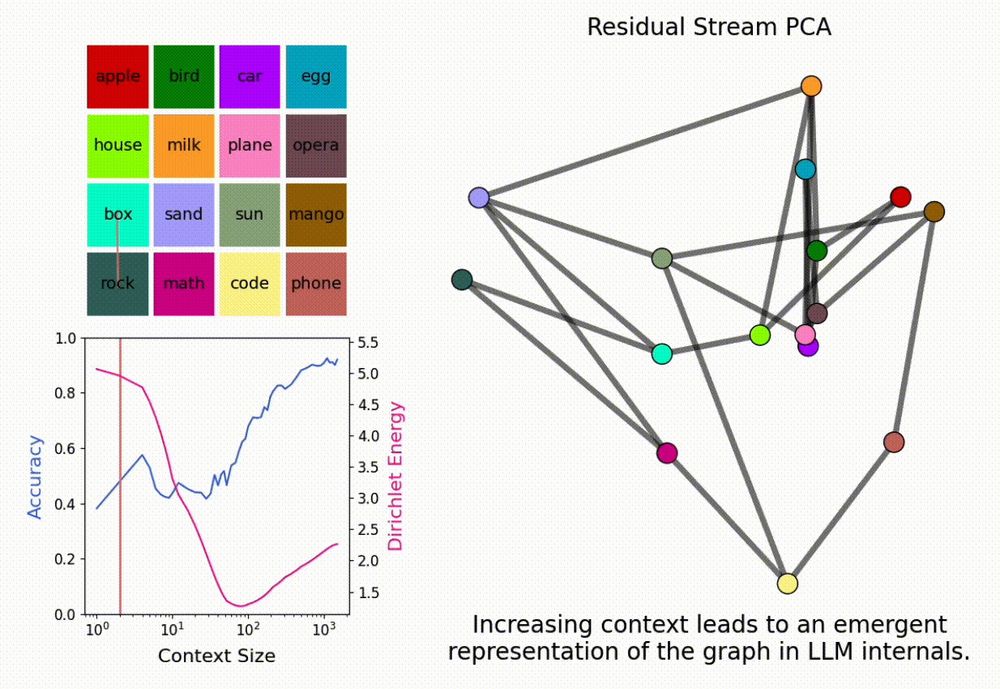
We build a graph with random words as nodes, randomly walk the graph, and input the resulting seq to LMs. With a long enough context, LMs start adhering to the graph
When this happens, PCA of LM activations reveals the graph (task) structure
3/N

We build a graph with random words as nodes, randomly walk the graph, and input the resulting seq to LMs. With a long enough context, LMs start adhering to the graph
When this happens, PCA of LM activations reveals the graph (task) structure
3/N
Team: @corefpark.bsky.social @ekdeepl.bsky.social YongyiYang MayaOkawa KentoNishi @wattenberg.bsky.social @hidenori8tanaka.bsky.social
arxiv.org/pdf/2501.00070
2/N

Team: @corefpark.bsky.social @ekdeepl.bsky.social YongyiYang MayaOkawa KentoNishi @wattenberg.bsky.social @hidenori8tanaka.bsky.social
arxiv.org/pdf/2501.00070
2/N
Interested in inference-time scaling? In-context Learning? Mech Interp?
LMs can solve novel in-context tasks, with sufficient examples (longer contexts). Why? Bc they dynamically form *in-context representations*!
1/N
Interested in inference-time scaling? In-context Learning? Mech Interp?
LMs can solve novel in-context tasks, with sufficient examples (longer contexts). Why? Bc they dynamically form *in-context representations*!
1/N

