Aaron Roth
@aaroth.bsky.social
Professor at Penn, Amazon Scholar at AWS. Interested in machine learning, uncertainty quantification, game theory, privacy, fairness, and most of the intersections therein
How should you use forecasts f:X->R^d to make decisions? It depends what properties they have. If they are fully calibrated (E[y | f(x) = p] = p), then you should be maximally aggressive and act as if they are correct --- i.e. play argmax_a E_{o ~ f(x)}[u(a,o)]. On the other hand

October 30, 2025 at 7:02 PM
How should you use forecasts f:X->R^d to make decisions? It depends what properties they have. If they are fully calibrated (E[y | f(x) = p] = p), then you should be maximally aggressive and act as if they are correct --- i.e. play argmax_a E_{o ~ f(x)}[u(a,o)]. On the other hand
The opportunities and risks of the entry of LLMs into mathematical research in one screenshot. I think it is clear that LLMs will make trained researchers more effective. But they will also lead to a flood of bad/wrong papers, and I'm not sure we have the tools to deal with this.

September 24, 2025 at 8:00 PM
The opportunities and risks of the entry of LLMs into mathematical research in one screenshot. I think it is clear that LLMs will make trained researchers more effective. But they will also lead to a flood of bad/wrong papers, and I'm not sure we have the tools to deal with this.
The paper is here: arxiv.org/abs/2509.15090 and is joint work with the excellent @ncollina.bsky.social , @surbhigoel.bsky.social , Emily Ryu, and Mirah Shi.




September 19, 2025 at 12:14 PM
The paper is here: arxiv.org/abs/2509.15090 and is joint work with the excellent @ncollina.bsky.social , @surbhigoel.bsky.social , Emily Ryu, and Mirah Shi.
I'm excited about this line of work. We get clean results in a stylized setting, and there is much to do to bring these kinds of ideas closer to practice. But I think that ideas from market and mechanism design should have lots to say about the practical alignment problem too.

September 19, 2025 at 12:14 PM
I'm excited about this line of work. We get clean results in a stylized setting, and there is much to do to bring these kinds of ideas closer to practice. But I think that ideas from market and mechanism design should have lots to say about the practical alignment problem too.
We conduct another simple experiment in which we explicitly compute equilibria amongst differently misaligned sets of agents. The results validate our theory --- user utility can sometimes match our worst case bound (so its tight), but is often much better.

September 19, 2025 at 12:14 PM
We conduct another simple experiment in which we explicitly compute equilibria amongst differently misaligned sets of agents. The results validate our theory --- user utility can sometimes match our worst case bound (so its tight), but is often much better.
We give simple experiments (where LLM personas are generated with prompt variation) demonstrating that representing user utility functions somewhere in the convex hull of LLM utility functions is a much easier target than finding a single well aligned LLM utility function.

September 19, 2025 at 12:14 PM
We give simple experiments (where LLM personas are generated with prompt variation) demonstrating that representing user utility functions somewhere in the convex hull of LLM utility functions is a much easier target than finding a single well aligned LLM utility function.
Even if all of the AI providers are very badly aligned, if it is possible to approximate the user's utility by any non-negative linear combination of their utilities, then the user does as well as they would with a perfectly aligned AI. Alignment emerges from competition.

September 19, 2025 at 12:14 PM
Even if all of the AI providers are very badly aligned, if it is possible to approximate the user's utility by any non-negative linear combination of their utilities, then the user does as well as they would with a perfectly aligned AI. Alignment emerges from competition.
We give several mathematical models of AI competition in which the answer is yes, provided that the user's utility function lies in the convex hull of the AI utility functions. Under this condition, all equilibria of the game between AI providers leads to high user utility.
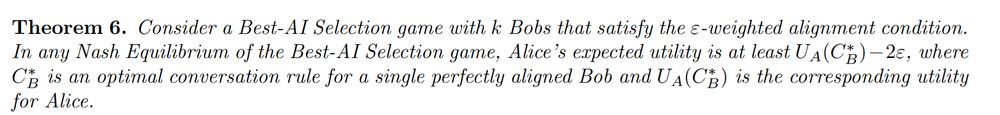
September 19, 2025 at 12:14 PM
We give several mathematical models of AI competition in which the answer is yes, provided that the user's utility function lies in the convex hull of the AI utility functions. Under this condition, all equilibria of the game between AI providers leads to high user utility.
Aligning an AI with human preferences might be hard. But there is more than one AI out there, and users can choose which to use. Can we get the benefits of a fully aligned AI without solving the alignment problem? In a new paper we study a setting in which the answer is yes.

September 19, 2025 at 12:14 PM
Aligning an AI with human preferences might be hard. But there is more than one AI out there, and users can choose which to use. Can we get the benefits of a fully aligned AI without solving the alignment problem? In a new paper we study a setting in which the answer is yes.
The paper is here: arxiv.org/abs/2507.09683 This is joint work with @mkearnsphilly.bsky.social and Emily Ryu, from a fun visit in June.


July 24, 2025 at 1:41 PM
The paper is here: arxiv.org/abs/2507.09683 This is joint work with @mkearnsphilly.bsky.social and Emily Ryu, from a fun visit in June.
Suppose we have a regression problem that many people want to solve, but information is distributed across agents --- different agents see different subsets of features. And the agents are embedded in a network (DAG). When one makes predictions, they are observed by its children.

July 24, 2025 at 1:41 PM
Suppose we have a regression problem that many people want to solve, but information is distributed across agents --- different agents see different subsets of features. And the agents are embedded in a network (DAG). When one makes predictions, they are observed by its children.
Agentic LLM tooling like Windsurf is amazing. But you can already tell from the interface (you can pick from two dozen models from half a dozen different model providers, seamlessly) that AI is going to be a commodity. Not at all clear that LLM developers will get the surplus.

June 11, 2025 at 11:40 PM
Agentic LLM tooling like Windsurf is amazing. But you can already tell from the interface (you can pick from two dozen models from half a dozen different model providers, seamlessly) that AI is going to be a commodity. Not at all clear that LLM developers will get the surplus.
The paper is here: arxiv.org/abs/2504.06075 and is joint work with the excellent @ncollina.bsky.social , @iraglobusharris.bsky.social , @surbhigoel.bsky.social , Varun Gupta, and Mirah Shi!

April 9, 2025 at 12:12 PM
The paper is here: arxiv.org/abs/2504.06075 and is joint work with the excellent @ncollina.bsky.social , @iraglobusharris.bsky.social , @surbhigoel.bsky.social , Varun Gupta, and Mirah Shi!
Just as our last paper generalized Aumann's agreement theorem, this paper tractably generalizes "information aggregation" theorems for Bayesian reasoners. Our results lift back to the classic Bayesian setting and give the first distribution free information aggregation theorems.

April 9, 2025 at 12:12 PM
Just as our last paper generalized Aumann's agreement theorem, this paper tractably generalizes "information aggregation" theorems for Bayesian reasoners. Our results lift back to the classic Bayesian setting and give the first distribution free information aggregation theorems.
For any function classes H(A), H(B), H(J) satisfying this weak learning condition, we show how two parties can collaborate to be as accurate at H(J), by only needing to solve a small number of squared error regression problems on their own data over H(A) and H(B) respectively.

April 9, 2025 at 12:12 PM
For any function classes H(A), H(B), H(J) satisfying this weak learning condition, we show how two parties can collaborate to be as accurate at H(J), by only needing to solve a small number of squared error regression problems on their own data over H(A) and H(B) respectively.
H(A) and H(B) are weak learners wrt H(J) if, whenever learning over H(J) can improve on constant prediction, learning over H(A) or H(B) can as well. It turns out linear functions over X(A) and linear functions over X(B) are weak learners wrt linear functions over the joint features.


April 9, 2025 at 12:12 PM
H(A) and H(B) are weak learners wrt H(J) if, whenever learning over H(J) can improve on constant prediction, learning over H(A) or H(B) can as well. It turns out linear functions over X(A) and linear functions over X(B) are weak learners wrt linear functions over the joint features.
In our new paper, what we show is that if both parties further have no swap regret (are "multicalibrated") with respect to function classes H(A), H(B) defined on their own features, then we can give accuracy guarantees with respect to a joint function class H(J).

April 9, 2025 at 12:12 PM
In our new paper, what we show is that if both parties further have no swap regret (are "multicalibrated") with respect to function classes H(A), H(B) defined on their own features, then we can give accuracy guarantees with respect to a joint function class H(J).
Suppose you and I both have different features about the same instance. Maybe I have CT scans and you have physician notes. We'd like to collaborate to make predictions that are more accurate than possible from either feature set alone, while only having to train on our own data.

April 9, 2025 at 12:12 PM
Suppose you and I both have different features about the same instance. Maybe I have CT scans and you have physician notes. We'd like to collaborate to make predictions that are more accurate than possible from either feature set alone, while only having to train on our own data.
Its interesting to see OpenAI slowly tighten the guardrails around the Studio Ghibli meme.


March 27, 2025 at 1:24 PM
Its interesting to see OpenAI slowly tighten the guardrails around the Studio Ghibli meme.
My first attempt at writing a Philosophy paper with Alex. Forthcoming in Philosophy of Science! We study the reference class problem which is about the indeterminacy of "individual probabilities" from data. What is the chance that Alice will die in the next 12 months? philsci-archive.pitt.edu/23589/

March 24, 2025 at 1:35 PM
My first attempt at writing a Philosophy paper with Alex. Forthcoming in Philosophy of Science! We study the reference class problem which is about the indeterminacy of "individual probabilities" from data. What is the chance that Alice will die in the next 12 months? philsci-archive.pitt.edu/23589/
A breakthrough in swap theory.

March 1, 2025 at 3:34 PM
A breakthrough in swap theory.
Alex Tolbert is running a stellar conference next week at Emory that I am bummed to be missing out on. The speaker lineup is especially remarkable- spanning theoretical computer science to machine learning to law to philosophy. You should go and enjoy it for me. 39893947.hs-sites.com/aiethicsconf...

February 25, 2025 at 9:58 PM
Alex Tolbert is running a stellar conference next week at Emory that I am bummed to be missing out on. The speaker lineup is especially remarkable- spanning theoretical computer science to machine learning to law to philosophy. You should go and enjoy it for me. 39893947.hs-sites.com/aiethicsconf...
Can you solve group-conditional online conformal prediction with a no-regret learning algorithm? Not with vanilla regret, but -yes- with swap regret. And algorithms from the follow-the-regularized leader family (notably online gradient descent) work really well for other reasons.

February 18, 2025 at 1:19 PM
Can you solve group-conditional online conformal prediction with a no-regret learning algorithm? Not with vanilla regret, but -yes- with swap regret. And algorithms from the follow-the-regularized leader family (notably online gradient descent) work really well for other reasons.
Also this is an incredibly wide confidence interval given the price.


February 14, 2025 at 6:52 PM
Also this is an incredibly wide confidence interval given the price.
Conflicted about whether to agree here

February 14, 2025 at 6:47 PM
Conflicted about whether to agree here

