TL;DR: Peak Selection is a novel mechanism for the modularity emergence in a variety of systems. Applied to grid cells, it makes testable predictions at molecular, circuit, and functional levels, and matches observed period ratios better than any existing model!
TL;DR: Peak Selection is a novel mechanism for the modularity emergence in a variety of systems. Applied to grid cells, it makes testable predictions at molecular, circuit, and functional levels, and matches observed period ratios better than any existing model!
Peak Selection applies broadly for module emergence:
The same mechanism can also explain:
🌱 Emergent ecological niches
🐠 Coral spawning synchrony
🤖 Modularity in optimization & learning
Peak Selection applies broadly for module emergence:
The same mechanism can also explain:
🌱 Emergent ecological niches
🐠 Coral spawning synchrony
🤖 Modularity in optimization & learning
Central results and predictions:
•Self-scaling with organism size
•Topologically robust: insensitive to almost all param variations, activity perturbations; also robust to weight heterogeneity! (no need for exactly symmetric interactions in CANs)
Central results and predictions:
•Self-scaling with organism size
•Topologically robust: insensitive to almost all param variations, activity perturbations; also robust to weight heterogeneity! (no need for exactly symmetric interactions in CANs)
Central results and predictions:
•Nearly **any** interaction shape can form grid cell patterning (Mexican-hat kernels not needed!)
•Grid cells involve two scales of interactions, one spatially varying and one fixed.
•Functional modularity can emerge without molecular modularity.
Central results and predictions:
•Nearly **any** interaction shape can form grid cell patterning (Mexican-hat kernels not needed!)
•Grid cells involve two scales of interactions, one spatially varying and one fixed.
•Functional modularity can emerge without molecular modularity.
Grid modularity from Peak Selection!
•Discrete jumps in grid period without discrete precursors.
•Novel period ratio prediction: adjacent periods ratios vary as ratio of integers (3/2, 4/3, 5/4, …).
•Excellent agreement with data (R^2 ~0.99)!
Grid modularity from Peak Selection!
•Discrete jumps in grid period without discrete precursors.
•Novel period ratio prediction: adjacent periods ratios vary as ratio of integers (3/2, 4/3, 5/4, …).
•Excellent agreement with data (R^2 ~0.99)!
Grid modularity from Peak Selection!
•Two forms of local interactions: one spatially varying smoothly in scale, the other held fixed.
•These spontaneously generate local patterning and global modularity!
Grid modularity from Peak Selection!
•Two forms of local interactions: one spatially varying smoothly in scale, the other held fixed.
•These spontaneously generate local patterning and global modularity!
2 classic ideas for structure emergence in biology
•Positional hypothesis: genes apply discrete thresholds, but discrete gene expression
•Turing hypothesis: Local interactions drive patterns, but single scale
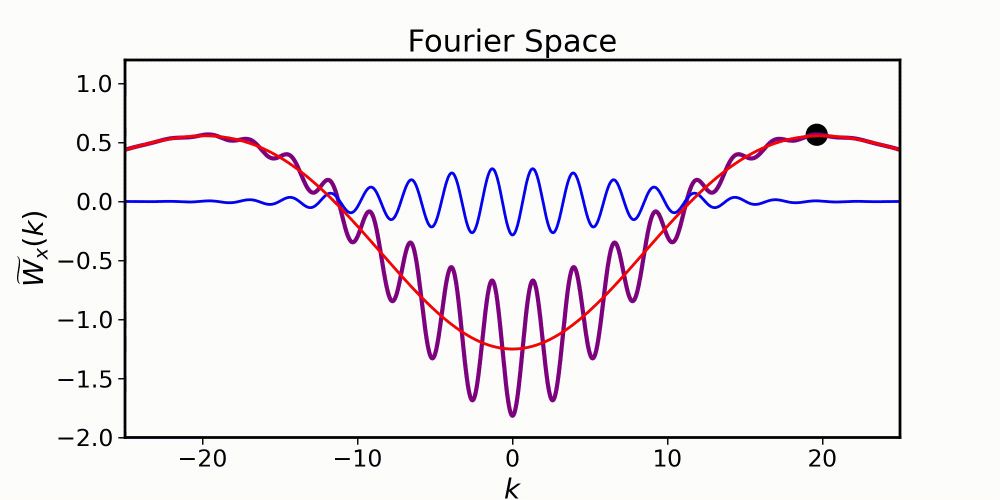
But grid modules are multiscale, from presumably continuous precursors
2 classic ideas for structure emergence in biology
•Positional hypothesis: genes apply discrete thresholds, but discrete gene expression
•Turing hypothesis: Local interactions drive patterns, but single scale
But grid modules are multiscale, from presumably continuous precursors
Various measured cellular and circuit properties vary smoothly across grid cells. Yet, grid cells are organized into discrete modules with different spatial periods. How does discrete organization arise from smooth gradients?
Various measured cellular and circuit properties vary smoothly across grid cells. Yet, grid cells are organized into discrete modules with different spatial periods. How does discrete organization arise from smooth gradients?
Hippocampal cells remap by direction/context 📍➡️⬅️
Memory consolidation of multiple memory traces 📚
Model thus bridges experiments and theory!
Hippocampal cells remap by direction/context 📍➡️⬅️
Memory consolidation of multiple memory traces 📚
Model thus bridges experiments and theory!
VectorHaSH mirrors entorhinal-hippocampal phenomena:
Grid cells demonstrate stable periodicity, rapid phase resets, robust velocity integration 🌐
Recreate correlation statistics of grid cells and place cells 📊
VectorHaSH mirrors entorhinal-hippocampal phenomena:
Grid cells demonstrate stable periodicity, rapid phase resets, robust velocity integration 🌐
Recreate correlation statistics of grid cells and place cells 📊
Why does imagining a spatial walk supercharge memory?
VectorHaSH shows how recall of familiar locations acts as a secondary scaffold.
Result: Even approximate recall of locations reliably supports one-shot arbitrary, high-fidelity memories. 💡
Why does imagining a spatial walk supercharge memory?
VectorHaSH shows how recall of familiar locations acts as a secondary scaffold.
Result: Even approximate recall of locations reliably supports one-shot arbitrary, high-fidelity memories. 💡
VectorHaSH then stores memories by heteroassociation of inputs with these scaffold states, enabling graceful degradation of memory detail with the number of stored memories over a vast number of inputs
VectorHaSH then stores memories by heteroassociation of inputs with these scaffold states, enabling graceful degradation of memory detail with the number of stored memories over a vast number of inputs
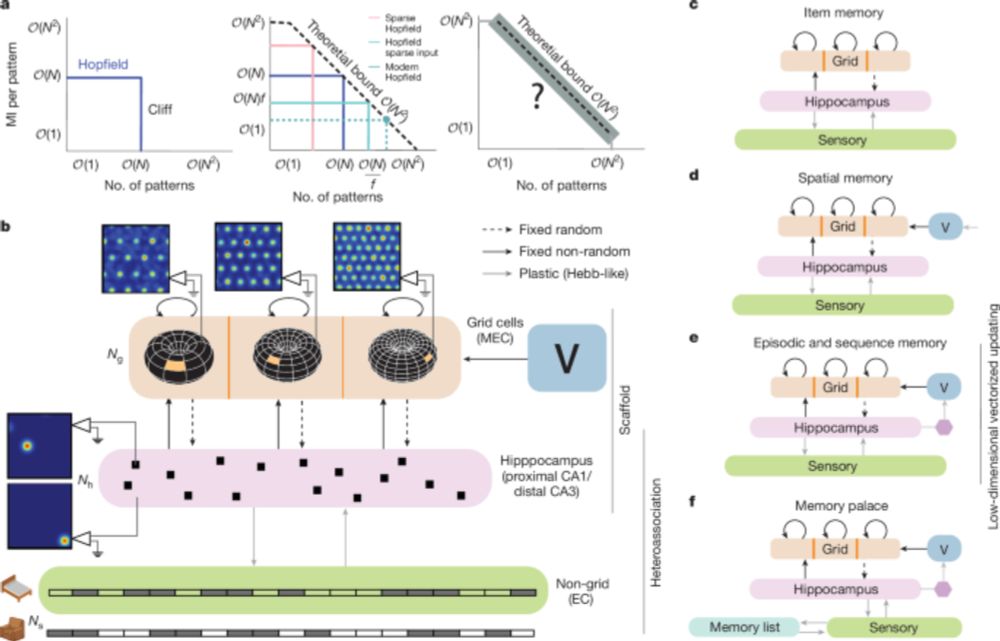
(3) Episodic memory, using low-dimensional transitions in the grid space to support massive sequence capacity 🎞️(4) Method of Loci, explaining the paradox of why adding to the memory task (associating items with spatial locations) boosts performance 🏰
(3) Episodic memory, using low-dimensional transitions in the grid space to support massive sequence capacity 🎞️(4) Method of Loci, explaining the paradox of why adding to the memory task (associating items with spatial locations) boosts performance 🏰
VectorHaSH supports: (1) Item memory, avoiding memory cliffs of Hopfield nets (2) Spatial memory, learning landmark-location associations over many maps 🌍& minimizing catastrophic forgetting
VectorHaSH supports: (1) Item memory, avoiding memory cliffs of Hopfield nets (2) Spatial memory, learning landmark-location associations over many maps 🌍& minimizing catastrophic forgetting

