Latest novel: MORPHOTROPHIC
Latest collection: SLEEP AND THE SOUL
Web site: http://gregegan.net
Also: @[email protected]

But what about the 3D equivalent?
Start with an ellipse and a hyperbola in orthogonal planes, with each curve’s vertices being the other’s foci.
But what about the 3D equivalent?
Start with an ellipse and a hyperbola in orthogonal planes, with each curve’s vertices being the other’s foci.
Congratulations to Georgina Steytler, who just won a wildlife photography award for this extraordinary image!
www.abc.net.au/news/2025-10...

Congratulations to Georgina Steytler, who just won a wildlife photography award for this extraordinary image!
www.abc.net.au/news/2025-10...


“Spare Parts for the Mind”

“Spare Parts for the Mind”


Explorer Books: explorerbooks.org/product/cloc...
About the Orthogonal Trilogy:
www.gregegan.net/ORTHOGONAL/O...

Explorer Books: explorerbooks.org/product/cloc...
About the Orthogonal Trilogy:
www.gregegan.net/ORTHOGONAL/O...
2030: Wait ... why did that bridge fall down?

2030: Wait ... why did that bridge fall down?
This was not one of them!
![Mathematica input: Assuming[R > 0 && M > 0 && 2 M < R,
FullSimplify[
Series[
Sqrt[2] R ArcTan[(Sqrt[R] - Sqrt[R - 2 M])/Sqrt[2 M]] -
Sqrt[M (R - 2 M)], {M, 0, 2}]]]
Output: (4*M^(3/2))/(3*Sqrt[R]) + O(M)^(5/2)](https://cdn.bsky.app/img/feed_thumbnail/plain/did:plc:nyxiyurvidf33xn5bcsotkvc/bafkreihjdsaew745s4vfod724base56ps6cy4g5zxickrmmvy7lmbgd7by@jpeg)
This was not one of them!
“Subscribe unless you want all humans dead forever.”
alignmentalignment.ai/caaac/blog/e...
(H/T @ mhoye @ mastodon dot social)
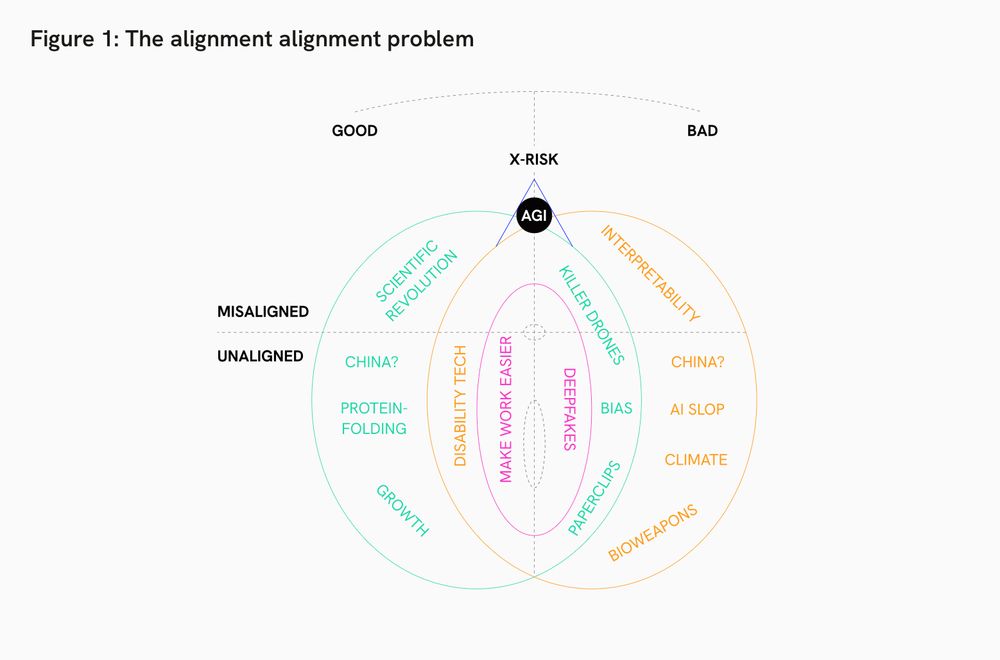
“Subscribe unless you want all humans dead forever.”
alignmentalignment.ai/caaac/blog/e...
(H/T @ mhoye @ mastodon dot social)

(R-3r)(R+r)≥d^2
to:
(R-nr)(R+(n-2)r)≥d^2
where r, R are the radii of the inner and outer spheres, d is the distance between their centres, and n is the dimension. I proved this was sufficient in 2014, but I couldn’t prove that it was necessary.
(R-3r)(R+r)≥d^2
to:
(R-nr)(R+(n-2)r)≥d^2
where r, R are the radii of the inner and outer spheres, d is the distance between their centres, and n is the dimension. I proved this was sufficient in 2014, but I couldn’t prove that it was necessary.
π, arcos(–1/√5), or arcos(1/√5)
π, arcos(–1/√5), or arcos(1/√5)


But they've also figured out how to eat toxic cane toads safely. They make an incision into the stomach, then remove and eat the heart and liver.
Cute, or what?

But they've also figured out how to eat toxic cane toads safely. They make an incision into the stomach, then remove and eat the heart and liver.
Cute, or what?
A graphics and material-modelling tool that can systematically handle impossible objects.
Want your Penrose triangles smoothed into bagels, while retaining their delicious impossibility? Meschers can do that.
H/T @[email protected]
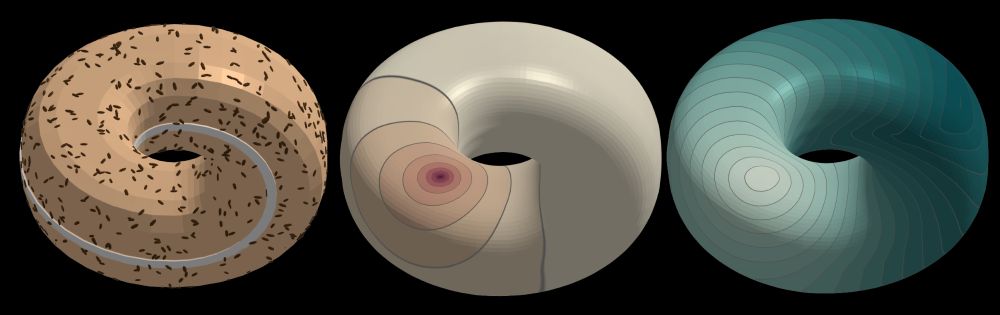
A graphics and material-modelling tool that can systematically handle impossible objects.
Want your Penrose triangles smoothed into bagels, while retaining their delicious impossibility? Meschers can do that.
H/T @[email protected]



