Paper: arxiv.org/abs/2408.01536
Code: github.com/dmusekamp/al...
9/

Paper: arxiv.org/abs/2408.01536
Code: github.com/dmusekamp/al...
9/
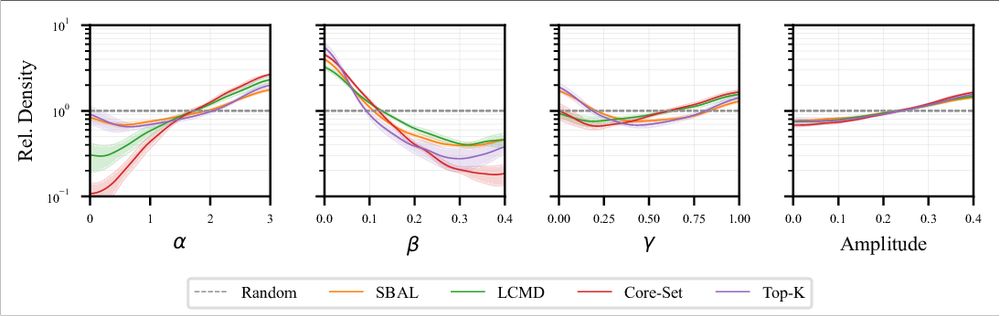
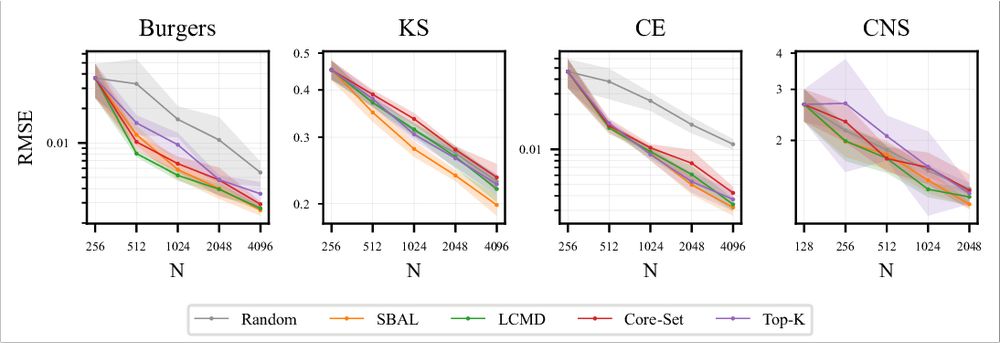
- Future work is needed to look at the missing advantage of AL on CNS.
- Benchmark does not include irregular grids or complex geometries, which might be
an interesting setting for AL due to the more complex input space. 8/
- Future work is needed to look at the missing advantage of AL on CNS.
- Benchmark does not include irregular grids or complex geometries, which might be
an interesting setting for AL due to the more complex input space. 8/
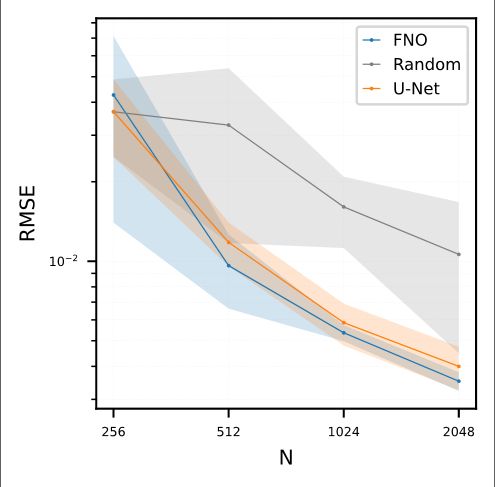
- Parametric PDEs such as incompressible Navier-Stokes
- Surrogate models (U-Net, FNO, SineNet).
- AL algorithms such as SBAL, CoreSet, or LCMD. 4/
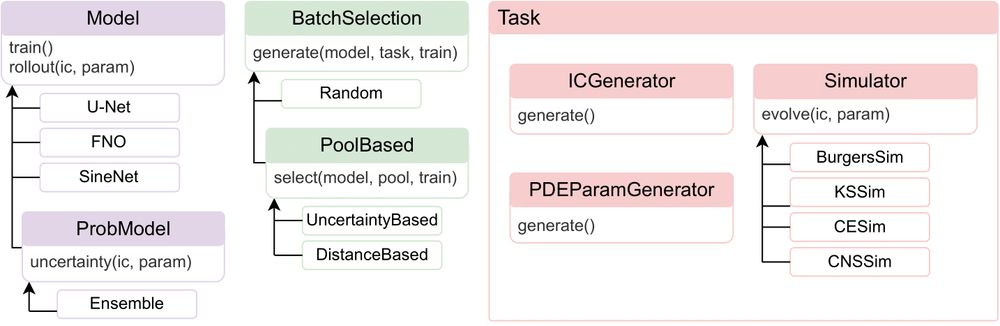
- Parametric PDEs such as incompressible Navier-Stokes
- Surrogate models (U-Net, FNO, SineNet).
- AL algorithms such as SBAL, CoreSet, or LCMD. 4/

